Калибровка потенциалов. Неоднородное уравнение Гельмгольца
Подставим соотношения найденные выражения векторов поля из потенциалов в первое уравнение Максвелла:
 .
.
Раскрывая операцию 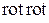 , получаем
, получаем
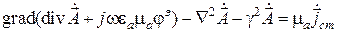
До сих по не накладывалось никаких ограничивающих условий на вид функций 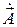 и
и 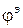 . Потребуем теперь, чтобы оба потенциала удовлетворяли следующему соотношению:
. Потребуем теперь, чтобы оба потенциала удовлетворяли следующему соотношению:
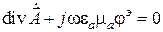
Данная формула носит название соотношения калибровки потенциалов. Из-за произвольного выбора функций 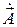 и
и 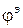 калибровочное соотношение может быть удовлетворено в любом случае.
калибровочное соотношение может быть удовлетворено в любом случае.
Заметим, что наложение условия калибровки значительно упрощает уравнение Максвелла с потенциалами, которое принимает вид
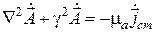
т. е. получается неоднородное уравнение Гсльмгольца относительно векторного электрического потенциала; в правой части его стоит известная функция распределения плотности стороннего электрического тока.
Отметим, что операция калибровки потенциалов позволяет выразить оба вектора электромагнитного поля через единственную функцию — электрический векторный потенциал. Действительно, воспользовавшись выражением калибровки, можно представить формулы перехода от потенциалов к векторам поля следующим образом:
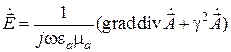 ,
,
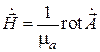 .
.
Дата добавления: 2015-10-19; просмотров: 1042;
