Второе уравнение Максвелла

Второе уравнение Максвелла является обобщением закона электромагнитной индукции Фарадея (Рисунок 31 ):

.

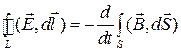Рисунок 32 − Произвольный контур в магнитном поле

В формулировке Фарадея считалось, что закон электромагнитной индукции справедлив только в случае проводящего контура 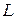, движущегося в постоянном электромагнитном поле, или неподвижного контура в переменном поле. Максвелл обобщил закон электромагнитной индукции, который в его формулировке звучит следующим образом:

Формулировка: ЭДС в произвольном замкнутом контуре пространства пропорциональна скорости изменения во времени потока магнитной индукции, пронизывающего любую поверхность, ограниченную контуром. Таким образом, уравнение справедливо и для произвольного замкнутого контура, проведенного в любой среде; в частном случае контур может быть проводящим, он может быть и воображаемым.

Дифференциальная форма уравнения получается, аналогично первому уравнению, применением к интегральной форме теоремы Стокса. Так как по теореме Стокса

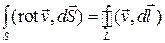
то, применяя ее к левой части второго уравнения Максвелла в интегральной форме, получим:

.

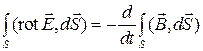Предположим, что контур 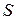неподвижен и не изменяется со временем. В этом случае производную по времени в правой части уравнения можно внести под знак интеграла:

.

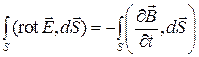Так как поверхность 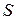произвольна, то это равенство возможно только при равенстве подынтегральных выражений, т.е.

,

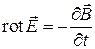что называется дифференциальной формой второго уравнения Максвелла.

В координатной форме второе уравнение Максвелла имеет вид:

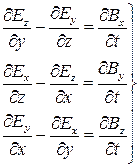
Второе уравнение Максвелла справедливо в любой точке пространства в любой момент времени и выражает обобщенный закон электромагнитной индукции в дифференциальной форме. Из этой формы уравнения следует, что изменение во времени в некоторой точке магнитного поля сопровождается изменением по пространственным координатам в той же точке электрического поля.