Третье уравнение Максвелла
Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность 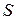 с зарядом
с зарядом 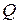 , сосредоточенным внутри нее:
, сосредоточенным внутри нее:
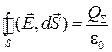 ,
,
так как 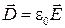 , то
, то
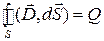 .
.
До Максвелла этот закон рассматривался только в применении к постоянным полям. Максвелл предположил, что это равенство справедливо и в случае переменных полей. Для заряда, распределенного внутри объема 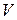 , который окружает поверхность
, который окружает поверхность 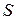 :
:
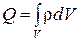 ,
,
подставляя это значение в закон Гаусса, получим
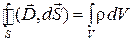
Это выражение называют третьим уравнением Максвелла в интегральной форме. Для перехода к дифференциальной форме используем теорему Остроградского-Гаусса:
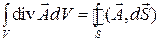
Преобразуем левую часть третьего уравнения Максвелла в соответствии с теоремой:
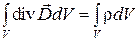 .
.
Это равенство должно выполняться при произвольном объеме 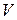 , что возможно только в том случае, если
, что возможно только в том случае, если
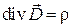 .
.
Из третьего уравнения Максвелла следует, что источником или стоком векторного поля 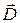 является плотность объемного электрического заряда, линии вектора
является плотность объемного электрического заряда, линии вектора 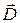 начинаются в точках, где
начинаются в точках, где 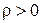 и заканчиваются в точках, где
и заканчиваются в точках, где 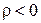 .
.
Координатная форма третьего уравнения для декартовой системы координат
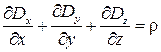 .
.
Дата добавления: 2015-10-19; просмотров: 1688;
