Обсуждение уравнений Максвелла

Вернемся к полной сводке уравнение Максвелла. Рассмотрение первых двух уравнений дает нам представление о строении электромагнитного поля.

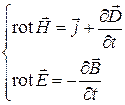
Из первого уравнения следует, что силовые линии магнитного поля охватывают линии полного тока, образуя с ними правовинтовую систему (). Аналогично, пространственный максимум магнитного потока охватывается семейством замкнутых электрических силовых линий.

Рисунок 34 − Строение электромагнитного поля

Первые два уравнения обладают симметрией в следующем смысле: по первому уравнению изменение во времени электрической индукции порождает вихревое магнитное поле, вектор напряженности которого изменяется в пространстве. По второму уравнению изменение во времени магнитной индукции порождает вихревое электрическое поле, изменяющееся в пространстве.

Из этого следует:

1. Электрическое поле может создаваться не только зарядом, но и переменным магнитным полем. Переменный магнитный поток неизбежно вызывает вихревое электрическое поле.

2. Магнитное поле возбуждается не только током проводимости, но и электрическим полем. Переменный по времени поток вектора электрической индукции 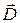неизбежно вызывает магнитное поле.

3. Электрическое и магнитное поля могут существовать, взаимно порождая друг друга. Например, если в некоторой области существует электрическое поле, то его изменение во времени (уменьшение или возрастание) приведет к появлению переменного магнитного поля. В свою очередь, изменяющееся магнитное поле вызовет вихревое электрическое поле. Происходит непрерывное взаимодействие между полями: одно поддерживает другое, и наоборот. Это определяет возможность существования электромагнитных волн в средах вдали от тел с токами проводимости.

Рисунок 35 − Возникновение электромагнитной волны

Физическая сущность такого процесса называется электромагнитной волной. Переменное электрическое поле 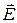в какой-то точке пространства вызывает, согласно первому уравнению, появление вокруг себя переменного магнитного поля 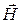. Это появившееся магнитное поле, в свою очередь, становясь причиной во втором уравнении, вызывает появление вокруг себя электрического поля и так далее. Схематически этот процесс показан на рисунке 34. Для получения полной картины поля во всем пространстве необходимо решить уравнения Максвелла.

Смысл третьего уравнения Максвелла прост, так как вполне исчерпывается понятиями дивергенции и потока вектора.

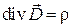
Линии вектора 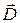начинаются на положительных и заканчиваются на отрицательных зарядах. Если же в какой-либо области пространства заряда нет 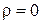, то характер силовых линий вектора 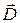должен соответствовать рисунку, т.е. количество линий «вошедших» в область, должно быть равно количеству «вышедших» и в этой области .

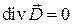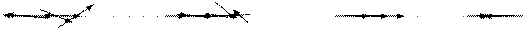
Рисунок 36 − Силовые линии вектора электрической индукции

Как следует из вывода третьего уравнения, его интегральная форма представляет собой теорему Гаусса:

.

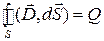Четвертое уравнение по форме отличается от третьего нулевой правой частью. В силу четвертого уравнения расхождение (дивергенция) вектора магнитной индукции везде равна нулю. Это означает, что магнитные силовые линии (линии вектора 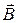) всегда непрерывны, т.е. либо замкнуты, либо идут из бесконечности в бесконечность. Характер картин магнитных силовых линий, таким образом, представлен на рисунке 36.

Рисунок 37 − Картина силовых линий магнитного поля

Непрерывность магнитных силовых линий указывает на отсутствие в природе фактора, который можно было бы называть «магнитным зарядом».