Сторонние токи и заряды
При рассмотрении уравнений Максвелла под вектором плотности тока 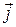 подразумевалась плотность тока проводимости, возникающего в проводящей среде под воздействием электромагнитного поля. Этот вектор удовлетворяет закону Ома в дифференциальной форме:
подразумевалась плотность тока проводимости, возникающего в проводящей среде под воздействием электромагнитного поля. Этот вектор удовлетворяет закону Ома в дифференциальной форме:
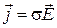 .
.
В рассматриваемой области пространства помимо этого тока могут существовать токи (источники), являющиеся первопричиной возникновения электромагнитного поля. Для того, чтобы принять их во внимание и не усложнить рассматриваемую модель, эти токи считаются заданными и вопрос об их возникновении не рассматривается. Примером такой задачи может служить излучение электромагнитных волн электрическим вибратором: ток, подведенный к вибратору от генератора, считается заданным, т.е. известным. При анализе это позволит исключить из рассмотрения все процессы, происходящие в генераторе, прохождение энергии по линии передачи от генератора к вибратору и т.д., что значительно упрощает задачу. Если этого не сделать, и каждый случай рассматривать во всей его полноте, то любая конкретная практическая задача становится трудноразрешимой.
Известные в задаче токи называют сторонними, и для их учета первое уравнение Максвелла записывается в виде:
 ,
,
то есть к сумме токов проводимости и смещения добавляется вектор плотности стороннего тока 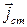 в рассматриваемой точке пространства, а
в рассматриваемой точке пространства, а 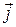 , как и прежде, плотность тока проводимости, вызванного электрическим полем:
, как и прежде, плотность тока проводимости, вызванного электрическим полем:
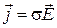 .
.
Примером источника стороннего тока является ток, протекающий в проводнике проволочной антенны, который при расчете поля антенны считается заданным. Зная напряжение, подведенное к проводу, можно рассчитать силу тока в каждой точке провода и задать плотность стороннего тока. При этом сами провода антенны становятся областью с источником стороннего тока. По этому известному стороннему току можно с помощью уравнений Максвелла рассчитать электромагнитное поле, излучаемой антенной в окружающее пространство.
Рисунок 38 − Сторонний ток в электрическом вибраторе
Весьма часто вместо сторонних токов используется сторонняя напряженность электрического поля 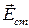 , под которой понимается напряженность электрического поля, создаваемая сторонними источниками, сосредоточенными за пределами рассматриваемой области. Пример стороннего электрического поля: рассмотрение антенны, находящей в падающей на нее плоской электромагнитной волне. При этом величина и направление вектора стороннего поля
, под которой понимается напряженность электрического поля, создаваемая сторонними источниками, сосредоточенными за пределами рассматриваемой области. Пример стороннего электрического поля: рассмотрение антенны, находящей в падающей на нее плоской электромагнитной волне. При этом величина и направление вектора стороннего поля 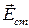 считаются заданным и известными. С помощью уравнений Максвелла в данном случае можно рассчитать ток проводимости, который образуется в антенне под воздействием стороннего поля
считаются заданным и известными. С помощью уравнений Максвелла в данном случае можно рассчитать ток проводимости, который образуется в антенне под воздействием стороннего поля 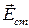 .
.
Введение 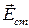 является таким же упрощением задачи, как и введение
является таким же упрощением задачи, как и введение 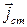 − оно позволяет исключить из анализа часть процессов, протекающих за пределами рассматриваемой области.
− оно позволяет исключить из анализа часть процессов, протекающих за пределами рассматриваемой области.
Аналогичным образом вводится понятие стороннего магнитного поля 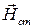
Учитывая все сторонние силы − сторонний ток 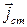 и стороннее электрическое поле
и стороннее электрическое поле 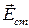 , первое уравнение Максвелла принимает вид:
, первое уравнение Максвелла принимает вид:

так как  , a
, a 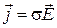 , то можем записать:
, то можем записать:
 ,
,
меняя местами слагаемые
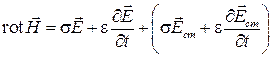 .
.
Можно ввести понятие полной плотности стороннего тока:
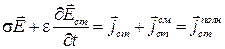
Аналогично вводятся понятия стороннего магнитного поля и сторонних зарядов.
Окончательно система уравнений Максвелла принимает вид:
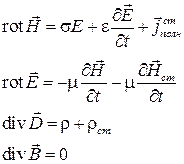
Дата добавления: 2015-10-19; просмотров: 2748;
