Односторонние производные функции в точке

Определение. Правой (левой) производной функции 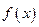в точке называется правый (левый) предел

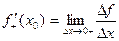
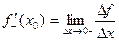
при условии, что этот предел существует.

Если функция 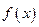имеет производную в некоторой точке , то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке 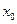, а во- вторых, даже если функция непрерывна в точке 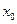, она может быть в ней не дифференцируема.

Например: 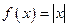- имеет в точке 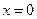и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема. (Необходимое условие существования производной) Если функция 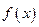имеет производную в точке 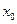, то она непрерывна в этой точке.

Очевидно, что это условие не является достаточным.