Производная функции, ее геометрический смысл
Определение. Производной функции 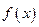 в точке
в точке  называется предел, если он существует, отношения приращения функции в точке
называется предел, если он существует, отношения приращения функции в точке  к приращению аргумента
к приращению аргумента 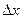 в этой точке, когда последнее стремится к нулю:
в этой точке, когда последнее стремится к нулю:
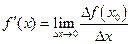 ,
,
где 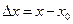 - приращение аргумента в точке
- приращение аргумента в точке 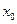 , а
, а 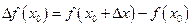 - соответствующее этому приращению приращение функции
- соответствующее этому приращению приращение функции 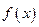 в этой точке.
в этой точке.
 у
у
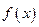
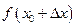 P
P
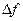
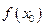 M
M
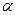
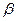
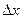
0 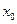
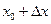 x
x
Пусть функция 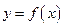 определена на некотором промежутке
определена на некотором промежутке 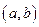 и имеет во внутренней точке
и имеет во внутренней точке  этого промежутка конечную производную. Пусть
этого промежутка конечную производную. Пусть 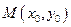 - точка графика функции
- точка графика функции 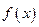 , соответствующая абсциссе
, соответствующая абсциссе  , а
, а 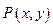 - произвольная точка графика функции.
- произвольная точка графика функции.
Касательной к кривой в точке  называется предельное положение секущей
называется предельное положение секущей 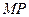 , когда точка
, когда точка 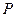 стремится к точке
стремится к точке 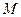 по кривой с любой стороны.
по кривой с любой стороны.
Обозначим через 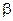 угол наклона секущей МР к положительному направлению оси
угол наклона секущей МР к положительному направлению оси 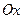 . Тогда
. Тогда 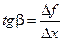 . Находим
. Находим
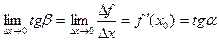 ,
,
где 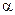 - угол наклона касательной к графику функции
- угол наклона касательной к графику функции 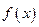 в точке
в точке 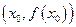 .
.
Угол между кривыми в их общей точке определяется как угол между касательными, проведенными к этим кривым в их общей точке.
Уравнение касательной к кривой в точке  имеет вид:
имеет вид: 
Уравнение нормали к кривой в точке  имеет вид:
имеет вид: 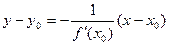 .
.
Функция 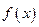 имеющая конечную производную в точке
имеющая конечную производную в точке 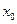 называется дифференцируемой в этой точке.
называется дифференцируемой в этой точке.
Дата добавления: 2015-09-29; просмотров: 636;
