Производная сложной функции. Теорема.Пусть , причем область значений функции входит в область определения функции .Тогда

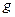Теорема.Пусть , причем область значений функции входит в область определения функции .Тогда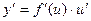

Доказательство. Имеем

.

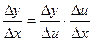Переходя к пределу в обеих частях при 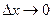получим:

,

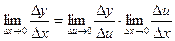(с учетом того, что если 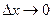, то 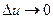, т.к. – непрерывная функция)

Тогда 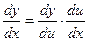. Теорема доказана.