Производная обратной функции

Пусть требуется найти производную функции 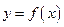при условии, что обратная ей функция 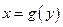имеет производную, отличную от нуля в соответствующей точке .

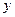Для решения этой задачи дифференцируем функцию 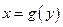по :

.

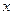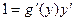Так как 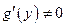, то

,

,

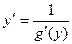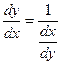т.е. производная обратной функции равна обратному значению данной функции.

Пример. Найти формулу для производной функции .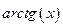

Функция 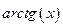является функцией, обратной функции 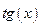, т.е. ее производная может быть найдена следующим образом:

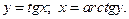
Известно, что 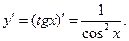Используя приведенную выше формулу получаем:

.

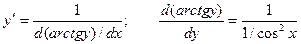Т.к. 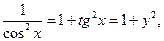то можно записать окончательную формулу для производной арктангенса:

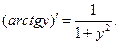
Аналогично получаются другие формулы для производных арксинуса, арккосинуса и других обратных функций, приведенные в таблице производных.