Дифференциал функции. Геометрический смысл дифференциала

Пусть функция 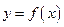имеет производную в точке :

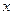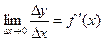
Тогда справедливо равенство: 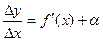, где , при .

Следовательно: .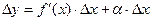

Величина 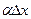является бесконечно малой более высокого порядка, чем 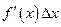, т.е. 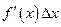- главная часть приращения .

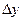Определение. Дифференциалом функции 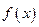в точке 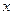называется главная линейная часть приращения функции. Обозначается 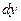или .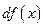

Из определения следует, что 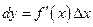или 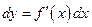, так как 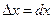. Следовательно, .

Геометрический смысл дифференциала.

y

K

M

L

x x

Из треугольника находим .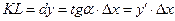

Таким образом, дифференциал функции 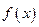в точке 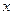равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.