Формула Маклорена

Формулой Маклоренаназывается формула Тейлора при :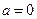

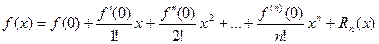
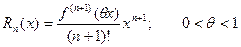
Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют.

Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно.

Другими словами, чем больше по модулю значение разности 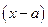тем более точное значение функции отличается от найденного по формуле Тейлора.

Кроме того, можно показать, что остаточный член 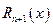является бесконечно малой функцией при 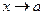, причем долее высокого порядка, чем 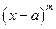, т.е.

.

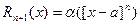Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.