Производная показательно- степенной функции
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть 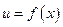 и
и 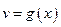 – функции, имеющие производные в точке
– функции, имеющие производные в точке 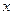 ,
, 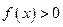 .
.
Найдем производную функции 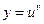 . Логарифмируя, получим:
. Логарифмируя, получим:
 ,
,
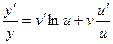 ,
,
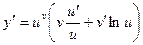 ,
,
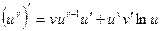 .
.
Пример. Найти производную функции  .
.
По полученной выше формуле получаем: 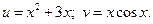
Производные этих функций: 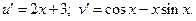
Окончательно:
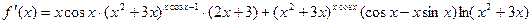 .
.
Дата добавления: 2015-09-29; просмотров: 941;
