Односторонние пределы

Определение предела функции

Одним из основных в математике является понятие предела, связанное с поведением функции при изменении аргумента, т.е. как именно величина функции меняется при изменении аргумента.

Рассмотрим функцию 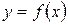непрерывно изменяющегося
аргумента х. Пусть х стремится к некоторому числу ( 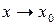). Введем понятие окрестности точки .

Определение.

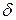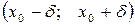−окрестностью точки называется интервал , где 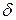−некоторое положительное число.

Если 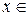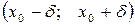, то выполняется неравенство 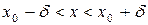, или, что то же, 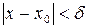. Выполнение последнего неравенства означает попадание точки х в 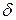−окрестность точки (рис. 2.1).

0 δ δ

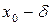
х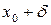

Рис. 2.1

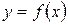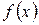Рассмотрим поведение функции вблизи точки . Считаем, что функция определена в некоторой окрестности точки , кроме, быть может, самой точки . Пусть при неограниченном приближении аргумента х к значения функции неограниченно приближаются к числу А. Это записывается так: 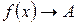при 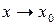. Данный факт означает, что с приближением х к разность 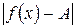становится как угодно малой и, какое бы число 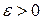не было выбрано заранее, наступит такой момент в изменении 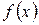, когда будет выполняться неравенство

.

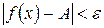В данном случае рассматриваются значения функции 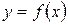при значениях аргумента х, близких к и не равных , т.е. для х, лежащих в интервале 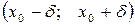, что равносильно выполнению неравенства

.

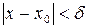Утверждение « 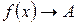, если 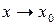» означает, что для любого заранее заданного положительного числа 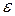можно найти такой интервал 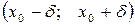около точки , что для всех 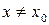из этого интервала, выполняется неравенство .

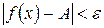Очевидно, что величина δ зависит от выбора 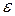, поэтому пишут 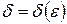. Если функция 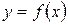изменяется именно так при 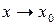, то
число А называется пределом функци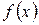и при .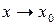

Определение.

Число А называется пределом функции в точке (или при 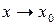), если для любого положительного числа 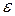, найдется такое положительное число δ, зависящее от 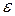, что для всех 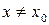и, удовлетворяющих неравенству 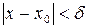, выполняется неравенство .

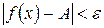Записывают:

.

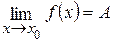Иными словами, числовые значения функции 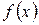будут заключены в произвольной 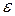−окрестности числа А при условии, что числовые значения аргумента х взяты в достаточно малой δ−окрестности числа (исключая само число ). Из определения следует, что закон, по которому 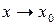, безразличен: х может стремиться к возрастая или убывая, или колеблясь около .

Точка называется предельной точкой.

Поясним понятие предела геометрически. Если 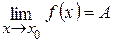, то для всех точек 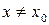, отстоящих от точки не далее чем на δ, точки графика функции 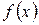лежат внутри полосы шириной 2 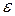, ограниченной прямым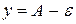и и 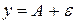(рис.2.2).

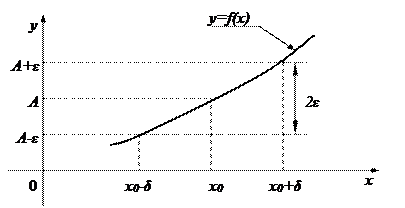Рис. 2.2

Односторонние пределы

В определении предела функции аргумент х принимает значения из окрестности точки , как слева, так и справа от , кроме .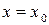

Однако, есть функции, поведение которых вблизи некоторой точки , существенно зависит от того, рассматриваются ли точки х, лежащие правее или левее точки . Поэтому вводят понятие односторонних пределов.

Определение.

Число 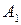называется пределом функции 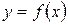слева в точке , если для любого числа 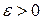существует число 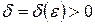такое, что при 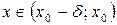, выполняется неравенство .

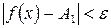Предел слева обозначают:

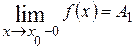или 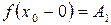(рис.2.3).

Определение.

Число 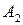называется пределом функции 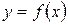справа в точке , если для любого числа 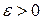существует число 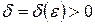такое, что при 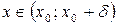, выполняется неравенство .

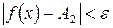Предел справа обозначают:

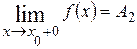или 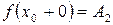(рис.2.3).

Рис. 2.3

Например, для функции

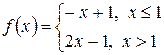
в точке 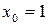имеем:

предел слева −

,

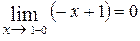предел справа −

.

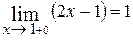Числа 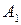и 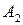характеризуют поведение функции 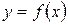, соответственно в левой [ 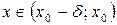] и правой [ 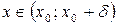] полуокрестности точки , поэтому пределы слева и справа называют односторонними пределами.

Если 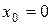, то предел слева функции 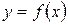обозначают

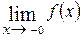или ,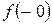

а предел справа −

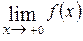или .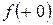

Если функция 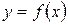задана на отрезке 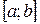или на интервале 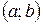, то в точке 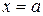функция может иметь только предел справа, а в точке 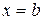− только предел слева.