Частные случаи электромагнитных процессов

Система уравнение Максвелла описывает всю совокупность электромагнитных явлений, относящихся к электродинамике. В ряде частных случаев уравнения Максвелла упрощаются. В связи с этими упрощениями электромагнитные поля подразделяются следующим образом.

Самыми простыми являются статические поля: неизменные во времени при отсутствии токов, то есть 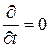, 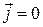. Тогда полная система уравнений распадается на две независимые системы. Первая из них, записанная в дифференциальной и интегральной формах

, ,

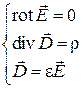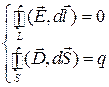описывает электростатическое поле, т.е. поле неподвижных и неизменных по величине зарядов, и называется системой дифференциальных уравнений электростатики. Вторая система

,
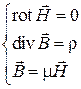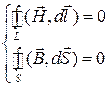
характеризует магнитостатическое поле, т.е., поле, создаваемое неподвижными постоянными магнитами. Эта система может быть также использована для анализа свойств магнитного поля, созданного постоянными токами в области, в которой плотность тока равна нулю, и которая не сцеплена с током (не охватывает его линий).

Первая из приведенных систем содержит только электрические величины, а вторая – только магнитные. Это означает, что для статических полей электрические и магнитные явления (поля) независимы.

Если же оставить только требование стационарности, т.е. 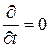, то это означает наличие постоянного тока. При этом электрическое и магнитное поля уже нельзя считать независимыми. Электромагнитное поле, созданное постоянными токами, называют стационарным полем и система уравнений Максвелла в этом случае принимает вид:

, ,

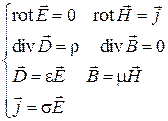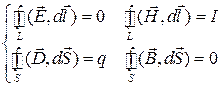
Уравнения, описывающие электрическое поле (левый столбец), не отличаются от уравнений электростатики, но теперь они не являются независимыми. Действительно, с напряженностью 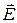связан вектор плотности тока 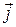, который также входит в уравнение из правого столбца. Записанные уравнения характеризуют электрическое и магнитное поля при наличии постоянного тока в общем случае.

Быстропеременные электромагнитные поля. Описываются полной системой уравнений Максвелла. При этом, в случае гармонических колебаний, система упрощается с помощью искусственного приема, получившего название «комплексных амплитуд».