Комплексные диэлектрическая и магнитная проницаемость

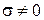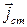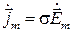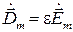Пусть среда имеет конечную проводимость и сторонние токи отсутствуют . Учтем, что и . Тогда в комплексной форме первое уравнение Максвелла запишется в виде

.

Вводя обозначение

,

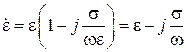получим

.

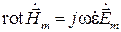Как видно, величина 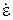по тому месту, которое она занимает в уравнении, может рассматриваться в качестве диэлектрической проницаемости. Это так называемая комплексная абсолютная диэлектрическая проницаемость. Она зависит от проводимости среды, ее диэлектрической проницаемости и частоты. Преобразуем выражение для нее к виду

.

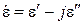Комплексная диэлектрическая проницаемость также часто обозначается в виде эпсилон с тильдой: .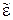

Значение реальной части комплексной диэлектрической проницаемости говорит об интенсивности процесса поляризации, в то время как мнимая часть характеризует плотность токов проводимости.

Отношение реальной и мнимой частей комплексной диэлектрической проницаемости равно отношению амплитуд плотностей тока смещения и тока проводимости и называется тангенсом угла электрических потерь. Комплексные амплитуды векторов плотности тока проводимости и плотности тока смещения равны соответственно 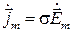и 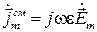, тогда

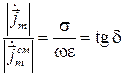
Рисунок 39 − Комплексная диэлектрическая проницаемость

Чем больше этот угол, тем большая часть электромагнитной энергии рассеивается в виде тепла.

Тангенс угла потерь определяет свойства среды в гармоническом электромагнитном поле и является критерием деления сред на проводники и диэлектрики:

1. 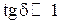, т.е. 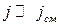− среда хорошо проводящая

2. 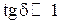, т.е. 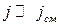− среда близка к диэлектрику

3. 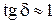, т.е. 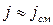−среда полупроводящая.

В силу частотной зависимости тангенса угла потерь, одна и та же среда на разных частотах может быть хорошо проводящей, полупроводящей и слабопроводящей (диэлектриком). С увеличением частоты все среды приобретают свойства диэлектрика. Металлы во всем диапазоне радиотехнических частот ведут себя как проводники.