Четвертое уравнение Максвелла

Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора магнитной индукции через любую замкнутую поверхность 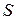равен нулю, т.е.

.

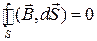Это уравнение является четвертым уравнением Максвелла и называется также принципом непрерывности магнитного потока. В дифференциальной форме четвертое уравнение Максвелла получается, аналогично третьему, с помощью теоремы Остроградского-Гаусса:

,

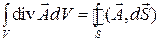тогда

,

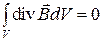а так как объем 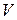может быть любым, то это равенство может выполняться только при

.

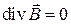Рисунок 33 − Линии вектора магнитной индукции

Физически смысл этого закона заключается в неразрывности магнитных силовых линий, что было установлено экспериментально. Из замкнутости силовых линий следует, что поток, «втекающий» в объем 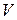, в точности равен потоку, «вытекающему» из этого же объема. Иначе говоря, не существует линий вектора 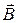, которые только входят, или, наоборот, только выходят из поверхности : они всегда пронизывают ее.