Выборочное уравнение нелинейной регрессии

Функции регрессии Y на X могут иметь вид, например, параболической корреляции второго порядка

, (7.10)

параболической корреляции третьего порядка

,

где A, B, C, D – неизвествные параметры.

Определить неизвестные параметры можно МНК. Для уравнения (7.9) неизвестные параметры A, B, C находят из решения системы линейных уравнений:

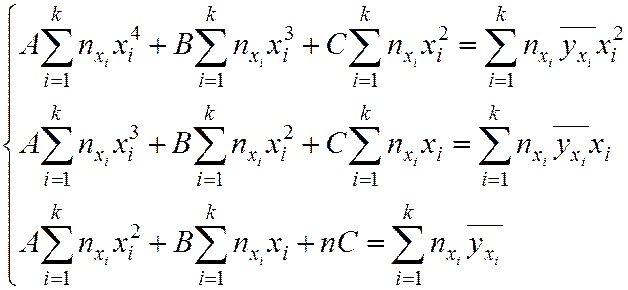
Пример. В. Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике», стр. 276.

Элементы дисперсионного анализа

Общие сведения

Дисперсионный анализ применяют, чтобы установить:

- оказывает ли существенное влияние некоторый качественный фактор 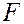, который имеет 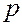уровней 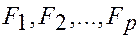на изучаемую величину ;

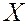- являются ли однородными несколько совокупностей, т.к. однородные совокупности можно объединить в одну и тем самым получить о ней более полную информацию.

Суть дисперсионного анализасостоит в сравнении «факторной дисперсии» (т.е. межгрупповой), обусловленной воздействием фактора, и «остаточной дисперсии» (т.е. внутригрупповой), порождаемой случайными причинами по критерию Фишера-Снедекора.

Различают дисперсионный анализ:

- однофакторный, если исследуется влияние одного фактора на изучаемую СВ;

- многофакторный, если исследуется воздействие нескольких факторов.

Рассмотрим случай однофакторного дисперсионного анализа, когда на изучаемую величину 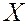влияет только один фактор, который имеет 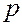постоянных уровней.