Аппроксимация модели методом наименьших квадратов (МНК). Свойства коэффициентов регрессии. Условия применения метода наименьших квадратов.
Понятие парной регрессии.
Регрессией в теории вероятностей и математической статистике принято называть зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин 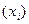 .
.
Парной регрессией называется модель, выражающая зависимость среднего значения зависимой переменной y от одной независимой переменной х
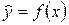 (2.1)
(2.1)
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак–фактор).
Парная регрессия применяется, если имеется доминирующий фактор, обуславливающий большую долю изменения изучаемой объясняемой переменной, который и используется в качестве объясняющей переменной.
Множественной регрессией называют модель, выражающую зависимость
среднего значения зависимой переменной y от нескольких независимых переменных 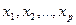 .
.
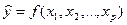 . (2.2)
. (2.2)
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать одновременное влияние нескольких факторов.
Используя уравнение регрессии (2.1), соотношение между значениями переменными у и х (модель связи) можно записать как
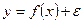 (2.3)
(2.3)
где первое слагаемое 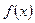 можно интерпретировать как ту часть значения y, которая объяснена уравнением регрессии (2.1), а второе слагаемое
можно интерпретировать как ту часть значения y, которая объяснена уравнением регрессии (2.1), а второе слагаемое 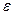 как необъясненную часть значения y (или возмущение). Соотношение между этими частями характеризует качество уравнения регрессии, его способность представлять зависимость между переменными х и y. При построении уравнения регрессии
как необъясненную часть значения y (или возмущение). Соотношение между этими частями характеризует качество уравнения регрессии, его способность представлять зависимость между переменными х и y. При построении уравнения регрессии 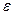 рассматривается как ошибка модели, представляющая собой случайную величину, удовлетворяющую определенным предположениям.
рассматривается как ошибка модели, представляющая собой случайную величину, удовлетворяющую определенным предположениям.
Наличие составляющей 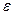 обусловлено такими причинами, как наличие дополнительных факторов, оказывающих влияние на переменную y, неверный
обусловлено такими причинами, как наличие дополнительных факторов, оказывающих влияние на переменную y, неверный
вид функциональной зависимости 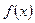 , ошибки измерения, выборочный характер исходных данных.
, ошибки измерения, выборочный характер исходных данных.
По виду аналитической зависимости различают линейные и нелинейные
регрессии.
Линейная парная регрессия описывается уравнением:
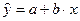 (2.4)
(2.4)
Примеры наиболее часто используемых нелинейных регрессий:
– полиномы разных степеней 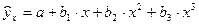 ,
,
– равносторонняя гипербола 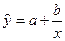 ,
,
– степенная 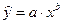 ,
,
– экспоненциальная 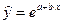 ,
,
– показательная 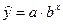 ,
,
– логистическая 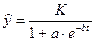 .
.
Дата добавления: 2015-11-06; просмотров: 2281;
