Применение метода дисперсионного анализа
Пусть ГС 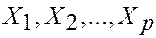 распределены нормально и имеют одинаковую, хотя и неизвестную, дисперсию; МО также неизвестны, но могут быть различными. Требуется при заданном
распределены нормально и имеют одинаковую, хотя и неизвестную, дисперсию; МО также неизвестны, но могут быть различными. Требуется при заданном 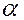 по выборочным средним проверить гипотезу
по выборочным средним проверить гипотезу 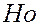 :
:
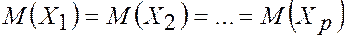
о равенстве всех МО. Другими словами требуется установить, значимо или незначимо, различаются выборочные средние.
Для того, чтобы проверить эту гипотезу, достаточно проверить по критерию Фишера-Снедекера гипотезу 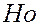 :
: 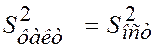 , если рассчитано, что
, если рассчитано, что 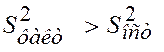 .
.
Если изначально 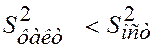 , то отсюда следует справедливость гипотезы о равенстве групповых средних.
, то отсюда следует справедливость гипотезы о равенстве групповых средних.
При проверке гипотезы о равенстве 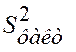 и
и 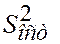 , если установлено, что они различаются значимо, то фактор
, если установлено, что они различаются значимо, то фактор 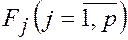 оказывает существенное влияние на СВ
оказывает существенное влияние на СВ 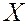 . А значит выборочные средние различаются также значимо.
. А значит выборочные средние различаются также значимо.
Если же установлено, что 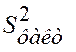 и
и 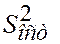 различаются незначимо, то гипотеза о равенстве средних не отвергается. При этом совокупности
различаются незначимо, то гипотеза о равенстве средних не отвергается. При этом совокупности 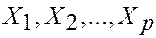 можно считать однородными.
можно считать однородными.
Пример.
Произведено 10 испытаний, из них 4 – на первом уровне, 4 – на втором и 2 – на третьем. Результаты испытаний приведены в таблице. Методом дисперсионного анализа проверить гипотезу о равенстве групповых средних при уровне значимости 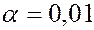 . Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора 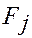
| ||
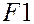
| 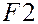
| 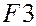
| |
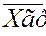
|
Решение
Для упрощения расчетов вычтем 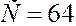 из каждого наблюдаемого значения
из каждого наблюдаемого значения 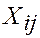 .
.
Составим расчетную таблицу.
| Номер испытания | Уровни фактора | Итоговый столбец | |||||
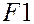
| 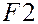
| 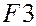
| |||||
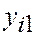
| 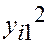
| 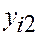
| 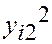
| 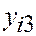
| 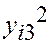
| ||
| -24 -20 -16 -28 | -2 | ||||||
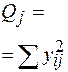
| 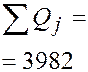
| ||||||
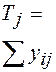
| -88 | 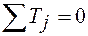
| |||||
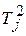
|
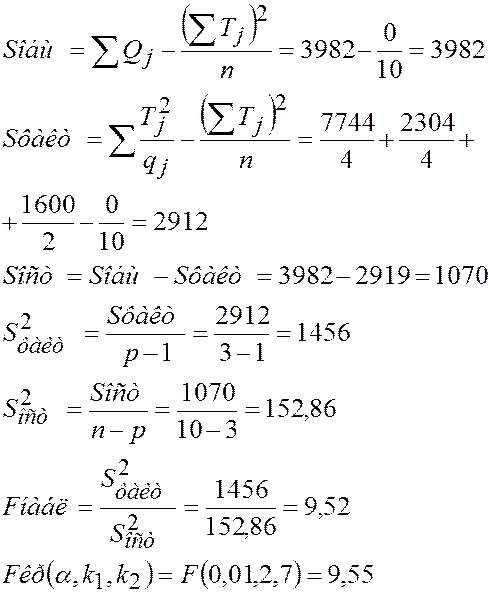
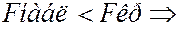 гипотезу
гипотезу 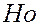 о равенстве средних не отвергаем: групповые средние отличаются незначимо.
о равенстве средних не отвергаем: групповые средние отличаются незначимо.
Дата добавления: 2015-11-18; просмотров: 878;
