Выборочный коэффициент корреляции
Точечная оценка тестоны линейной корреляционной взаимосвязи двух СВ X и Y, т. е. коэффициента корреляции, осуществляется с помощью выборочного коэффициента корреляции rв по формуле
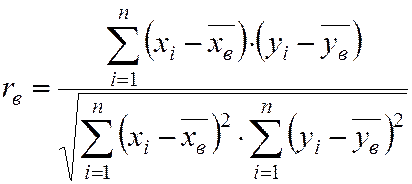 (6.1)
(6.1)
или
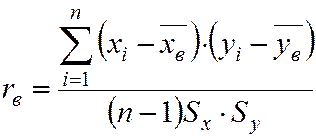 , n<30,
, n<30,
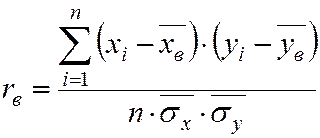 , n<30.
, n<30.
Пример.Установить силу корреляционной связи, если известны результаты наблюдений
| x | 1,00 | 1,50 | 3,00 | 4,50 | 5,00 |
| y | 1,25 | 1,40 | 1,50 | 1,75 | 2,25 |
Установим силу корреляционной связи. Для этого сначала произведём дополнительные вычисления:
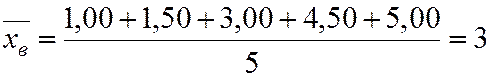 ;
;
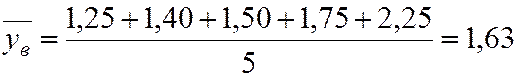 .
.
Вычислим средние квадратические отклонения:
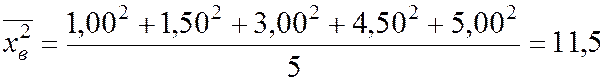 ;
; 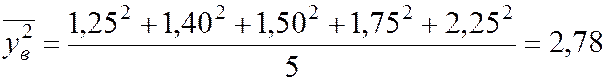 .
.
Тогда
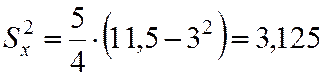 ;
;
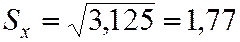 ;
;
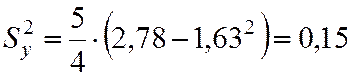 ;
;
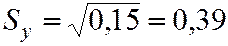 .
.
Полученные результаты подставляем в формулу (6.2) для вычисления выборочного коэффициента корреляции:
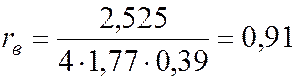 .
.
Выборочный коэффициент корреляции близок к единице, следовательно, корреляционная связь сильная.
При большом значение объёма выборки n одно и то же значение xi может встретиться 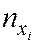 раз, yi –
раз, yi – 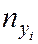 раз, одна и та же пара чисел
раз, одна и та же пара чисел 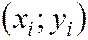 –
– 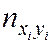 раз. Поэтому данные выборки группируют и записывают в виде т. н. корреляционной таблицы (табл. 6.1).
раз. Поэтому данные выборки группируют и записывают в виде т. н. корреляционной таблицы (табл. 6.1).
Таблица 6.1
| Y | ny | |||||
| x1 | … | xi | ... | xk | ||
| y1 | 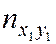
| … | 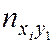
| … | 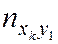
| 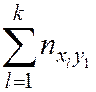
|
| … | … | … | … | … | … | … |
| yj | 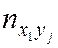
| … | 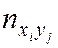
| … | 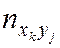
| 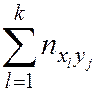
|
| … | … | … | … | … | … | … |
| ym | 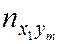
| … | 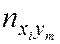
| … | 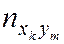
| 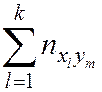
|
| nx | 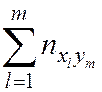
| … | 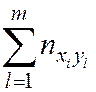
| … | 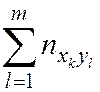
| n |
Тогда
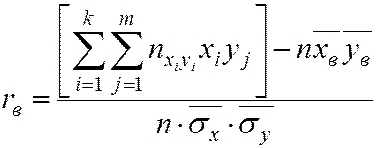 . (6.3)
. (6.3)
Если 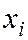 ,
, 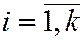 и
и 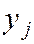 ,
, 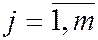 являются равноотстоящими с соответствующими значениями h1 и h2, то при расчете rв целесобразно перейти к условным вариантам.
являются равноотстоящими с соответствующими значениями h1 и h2, то при расчете rв целесобразно перейти к условным вариантам.
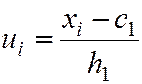 ,
, 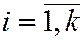 ; (6.4)
; (6.4)
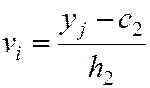 ,
, 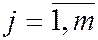 ,
,
где с1 – начало нового отсчёта величины X;
с2 – начало нового отсчёта величины Y;
h1 – расстояние между соседними вариантами величины X;
h2 – расстояние между соседними вариантами величины Y.
Тогда формула (6.3) примет вид
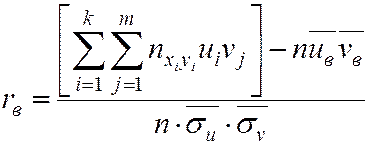 . (6.5)
. (6.5)
Абсолютное значение rв не превышает значение 1 ( 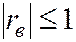 ).
).
Пример.Установить силу корреляционной святи, если результаті наблюдений
| Y | X | ny | ||||
| 20 | 25 | 30 | 35 | 40 | ||
| 16 | 4 | 6 | - | - | - | 10 |
| 26 | - | 8 | 10 | - | - | 18 |
| 36 | - | - | 32 | 3 | 9 | 44 |
| 46 | - | - | 4 | 12 | 6 | 22 |
| 56 | - | - | - | 1 | 5 | 6 |
| nx | 4 | 14 | 46 | 16 | 20 | n=100 |
Составляем корреляционную таблицу в условных вариантах. За ложные нули выбираем С1=30 и С2=36.
| U | V | nu | ||||
| -2 | -1 | 0 | 1 | 2 | ||
| -2 | 4 | 6 | - | - | - | 10 |
| -1 | - | 8 | 10 | - | - | 18 |
| 0 | - | - | 32 | 3 | 9 | 44 |
| 1 | - | - | 4 | 12 | 6 | 22 |
| 2 | - | - | - | 1 | 5 | 6 |
| nv | 4 | 14 | 46 | 16 | 20 | n=100 |
Находим 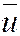 ,
, 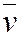 :
:
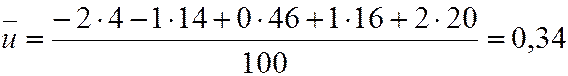 ;
;
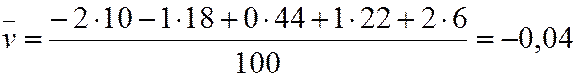 .
.
Найдём вспомогательные величины 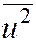 ,
, 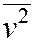 :
:
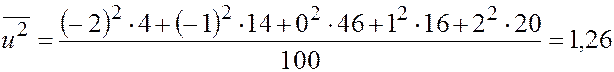
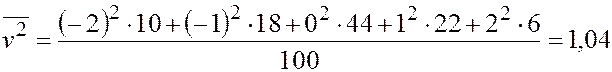
Вычисляем  ,
,  .
.
 .
.
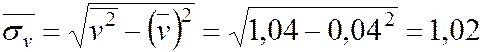 .
.
По формуле (6.5) находим выборочный коэффициент корреляции:
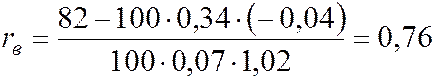 .
.
Значение rв далее может быть использовано для определения интервальной оценки коэффициента корреляции r. Например, интервальная оценка r нормально распределённой ГС при 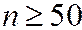 имеет вид
имеет вид
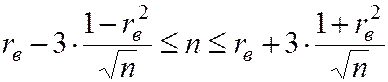 . (6.6)
. (6.6)
Известно, что если величины X и Y некоррелированы, то r=0 (Тема 4). Допустим, что 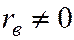 . Т. к. rв является оценкой, r то нельзя достоверно заключить, что r генеральной совокупности также отличен от 0.
. Т. к. rв является оценкой, r то нельзя достоверно заключить, что r генеральной совокупности также отличен от 0.
Поэтому возникает необходимость проверки статистической гипотезы 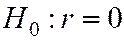 при конкурирующей гипотезе
при конкурирующей гипотезе 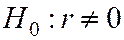 .
.
В качестве критерия для проверки основной гипотезы, если ГС (X, Y) распределена нормально, прнимают СВ
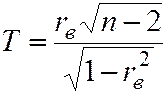 , (6.7)
, (6.7)
которая при справедливости H0 имеет распределение Стьюдента с числом степеней свободы, равным n-2.
Критическое значение критерия определяем по таблице критических точек распределения Стьюдента по заданному уровню значимости и числу степеней свободы. Наблюдаемое значение критерия определяем по формуле (6.7).
Если 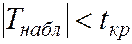 – нет оснований отвернуть H0, что означает: rв незначим, СВ X и Y не коррелированы.
– нет оснований отвернуть H0, что означает: rв незначим, СВ X и Y не коррелированы.
Если 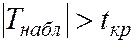 – H0 отвергают: rв значим, СВ X и Y коррелированы.
– H0 отвергают: rв значим, СВ X и Y коррелированы.
Дата добавления: 2015-11-18; просмотров: 8472;
