Параметры сред, классификация сред
Векторы 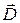 и
и 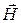 связаны с векторами
связаны с векторами 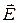 и
и 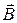 через макроскопические, т.е., усредненные параметры среды:
через макроскопические, т.е., усредненные параметры среды: 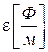 − электрическая проницаемость,
− электрическая проницаемость, 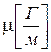 − магнитная проницаемость,
− магнитная проницаемость, 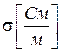 −удельная проводимость.
−удельная проводимость.
Параметры 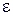 ,
, 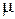 ,
, 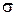 полностью характеризуют реакцию среды на электромагнитное поле, определяют макроскопические электромагнитные свойства среды. Диэлектрическая проницаемость
полностью характеризуют реакцию среды на электромагнитное поле, определяют макроскопические электромагнитные свойства среды. Диэлектрическая проницаемость 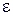 характеризует способность среды поляризоваться при воздействии электрического поля. Магнитная проницаемость
характеризует способность среды поляризоваться при воздействии электрического поля. Магнитная проницаемость 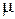 характеризует способность среды намагничиваться при воздействии магнитного поля. Удельная проводимость среды
характеризует способность среды намагничиваться при воздействии магнитного поля. Удельная проводимость среды 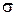 характеризует степень электропроводности.
характеризует степень электропроводности.
Связь между соответствующей парой векторов поля в веществе выражается через параметры 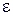 ,
, 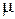 ,
, 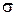 следующими уравнениями состояния:
следующими уравнениями состояния:
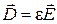 ,
, 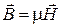 ,
, 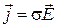 .
.
Макроскопические электромагнитные параметры среды определяются экспериментально.
В вакууме векторы 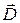 и
и 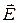 ,
, 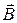 и
и 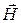 связаны соотношениями
связаны соотношениями
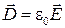 ,
, 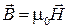 ,
,
где 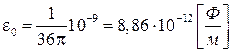 − диэлектрическая проницаемость свободного пространства (вакуума),
− диэлектрическая проницаемость свободного пространства (вакуума), 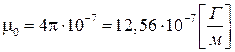 − магнитная проницаемость свободного пространства (вакуума).
− магнитная проницаемость свободного пространства (вакуума).
Часто, особенно в курсе антенн и устройств СВЧ, пользуются не абсолютными величинами диэлектрической и магнитной проницаемостей, а относительными, взятыми по отношению к 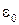 и
и 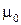 :
: 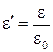 − относительная диэлектрическая проницаемость,
− относительная диэлектрическая проницаемость, 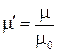 − относительная магнитная проницаемость.
− относительная магнитная проницаемость.
На рисунке 28 приведена фотография прибора Agilent E4991A, используемого для измерения параметров сред. Этот прибор есть у нас в институте.

Рисунок 28 − Прибор Agilent E4991A для определения параметров сред
В зависимости от свойств параметров 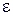 ,
, 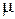 и
и 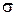 среды подразделяются на линейные и нелинейные.
среды подразделяются на линейные и нелинейные.
Линейные среды – среды, в которых параметры 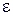 ,
, 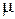 и
и 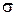 не зависят от величин и направлений электрического и магнитного полей; в этом случае зависимости
не зависят от величин и направлений электрического и магнитного полей; в этом случае зависимости 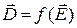 ,
, 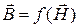 являются линейными ()
являются линейными ()
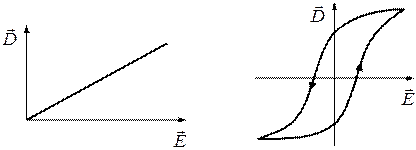
Рисунок 29 − Нелинейные и линейные среды
Нелинейные среды – среды, в которых параметры 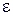 ,
, 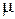 ,
, 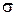 , или хотя бы один из них, зависят от величины электрического или магнитного полей. В этом случае соотношения
, или хотя бы один из них, зависят от величины электрического или магнитного полей. В этом случае соотношения 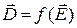 ,
, 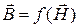 оказываются нелинейными функциями.
оказываются нелинейными функциями.
Строго говоря, все реальные среды являются нелинейными. Однако при не очень сильных полях в большинстве случаев, представляющих практический интерес, можно пренебречь зависимостью параметров 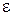 ,
, 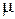 ,
, 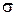 от величины электрического и магнитного полей и считать рассматриваемые среды линейными. В нашем курсе в дальнейшем мы будем рассматривать только линейные среды. Примерами нелинейных сред при слабых полях являются ферромагнетики (магнитная нелинейность) и сегнетоэлектрики (электрическая нелинейность).
от величины электрического и магнитного полей и считать рассматриваемые среды линейными. В нашем курсе в дальнейшем мы будем рассматривать только линейные среды. Примерами нелинейных сред при слабых полях являются ферромагнетики (магнитная нелинейность) и сегнетоэлектрики (электрическая нелинейность).
Линейные среды, в свою очередь, делятся на неоднородные и однородные, изотропные и неизотропные.
Однородными называют среды, параметры которых 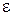 ,
, 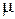 ,
, 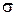 не зависят от координат, т.е., одинаковы во всех точках рассматриваемой среды.
не зависят от координат, т.е., одинаковы во всех точках рассматриваемой среды.
Неоднородными называют среды, у которых хотя бы один из параметров 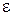 ,
, 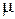 ,
, 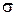 является функцией пространственных координат:
является функцией пространственных координат: 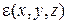 ,
, 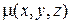 ,
, 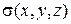 .
.
Изотропными называют среды, электромагнитные свойства которых одинаковы по всем направлениям, т.е. не зависят от направления векторов внешнего поля. Для изотропных сред параметры 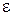 ,
, 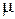 ,
, 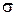 являются скалярами, а векторы
являются скалярами, а векторы 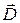 и
и 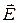 ,
, 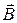 и
и 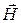 параллельны друг другу и связаны соотношениями
параллельны друг другу и связаны соотношениями
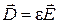 ,
, 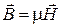 .
.
Подавляющее большинство сред относится к изотропным. Однако существует ряд сред, свойства которых существенно зависят от направления векторов внешнего электромагнитного поля. Такие среды называют анизотропными. В них пары векторов 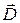 и
и 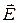 ,
, 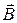 и
и 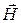 могут быть непараллельными и, по крайней мере, один из параметров
могут быть непараллельными и, по крайней мере, один из параметров 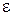 ,
, 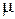 ,
, 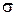 является тензором.
является тензором.
Например, вектор 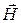 направлен по оси
направлен по оси 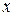 , т.е., имеет одну составляющую
, т.е., имеет одну составляющую 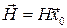 , а вектор
, а вектор 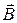 не совпадает по направлению с вектором
не совпадает по направлению с вектором 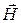 и имеет все три составляющие:
и имеет все три составляющие: 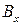 ,
, 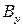 ,
, 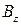 (рисунок 29). Каждая из составляющих вектора
(рисунок 29). Каждая из составляющих вектора 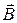 пропорциональна вектору
пропорциональна вектору 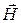 с разными коэффициентами пропорциональности
с разными коэффициентами пропорциональности 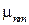 :
:
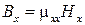 ,
, 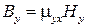 ,
, 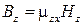 .
.
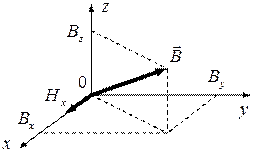
Рисунок 30 − Анизотропная система
В общем случае каждая проекция вектора 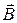 на оси координат зависит от всех трех составляющих вектора
на оси координат зависит от всех трех составляющих вектора 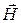 , связь между ними определяется системой уравнений:
, связь между ними определяется системой уравнений:
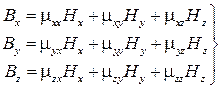
Таким образом, параметр 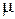 анизотропной ферромагнитной среды характеризуется девятью коэффициентами, записываемыми в виде матрицы − тензора:
анизотропной ферромагнитной среды характеризуется девятью коэффициентами, записываемыми в виде матрицы − тензора:
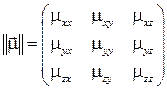 .
.
В этом случае векторы 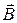 и
и 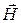 связаны соотношением
связаны соотношением
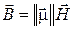 .
.
Аналогично для анизотропного диэлектрика
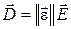 ,
,
где 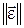 − тензор диэлектрической проницаемости.
− тензор диэлектрической проницаемости.
Примерами анизотропных сред являются кристаллы, намагниченные ферриты и др.
Следует отметить, что для большинства сред можно считать 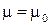 , и тогда
, и тогда 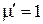 .
.
Дата добавления: 2015-10-19; просмотров: 3654;
