Векторный электрический потенциал для элементарного электрического излучателя

Пользуясь результатами рассмотрения электродинамических потенциалов, вычислим поле векторного электрического потенциала, возбуждаемого элементарным электрическим излучателем в неограниченном свободном пространстве ( , ).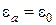

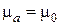В соответствии с физической постановкой данной задачи воспользуемся сферической системой координат 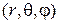, в начальной точке которой расположим излучатель. Ввиду малости геометрических размеров излучателя радиус-вектор 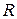, входящий в формулу для электродинамического потенциала 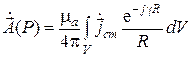, может считаться постоянным и равным сферической координате 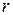. Отсюда будем иметь

.

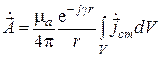Интегрирование вектора плотности стороннего тока по объему, занятому излучателем, представляет, на первый взгляд, логические трудности, поскольку, по определению, объем излучателя должен быть устремлен к нулю. Наиболее простой путь состоит в анализе физической размерности интеграла, входящего в последнюю формулу. Нетрудно проверить, что данный интеграл имеет размерность 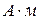. Здесь известны амплитуда стороннего электрического тока в излучателе 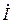и его длина .

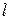Требуемая размерность будет получена, если положить 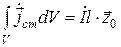, откуда

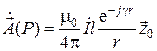
Единичный вектор i в двух последних формулах указывает на то, что ось элементарного излучателя направлена параллельно оси .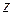

Для дальнейшего анализа необходимо знать разложение вектора 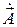в каждой точке пространства по ортам сферической системы координат. Способ подобного разложения показан на рисунке 74, из которого следует, что

,

.

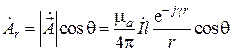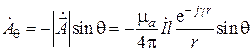Поскольку вектор электрического потенциала всюду направлен параллельно оси 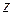, его проекция на направление азимутального угла тождественно равна нулю, т.е. .

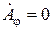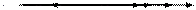
Рисунок 74 − Определение сферических проекций векторного потенциала