Решение неоднородного уравнения Гельмгольца

В данном разделе на основе простых физических соображений будет показан способ нахождения решения неоднородного уравнения Гельмгольца.

Предположим, что сторонние электрические токи локализованы в некотором объеме 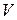(рисунок 72); интенсивность возбуждаемого поля должна быть определена в точке 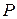, не принадлежащей .

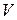Рисунок 72 − К решению неоднородного уравнения Гельмгольца

Рассмотрим элементарный объем 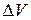, окружающий точку 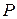, лежащую внутри 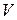. Очевидно, что интенсивность поля в точке наблюдения 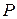, возникающего под действием токов, протекающих внутри 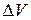, пропорциональна произведению 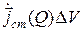. Здесь 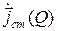— некоторое среднее значение плотности стороннего тока, которое можно считать постоянным внутри 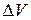из-за малости последнего.

Дальнейший путь решения уравнения Гельмгольца заключается в следующем. Ввиду линейности уравнений Максвелла рассматриваемая система удовлетворяет принципу суперпозиции. В соответствии с этим принципом полное решение неоднородного уравнения Гельмгольца может быть получено как сумма всех воздействий, вызываемых в точке 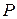отдельными элементарными объемами. С физической точки зрения ясно, что по своей природе данные воздействия представляют собой сферические волны, распространяющиеся из отдельных точек объема 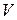и уносящие электромагнитную энергию на бесконечность. Ранее было указано, что комплексная амплитуда сферической волны записывается в виде

.

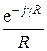Здесь, в соответствии с обозначениями, принятыми на рисунке 72, 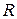− текущее значение модуля радиус-вектора, соединяющего точки 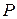и .

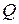Таким образом, с точностью до множителя пропорциональности величина элементарного воздействия

,

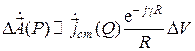откуда полная величина электрического векторного потенциала в точке наблюдения может быть найдена при помощи суммирования:

.

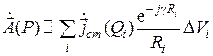Для того чтобы определить неизвестный коэффициент пропорциональности, необходимо совершить операцию предельного перехода, устремив к бесконечности число отдельных элементарных объемов. Как показано в курсе математической физики, строгий предельный переход

дает

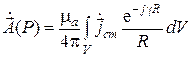
Таким образом, получено интегральное представление общего решения неоднородного уравнения Гельмгольца.