Решение неоднородных уравнений Максвелла

Во всех случаях, рассмотренных ранее, изучались так называемые однородные задачи электродинамики. При этом источники электромагнитного поля предполагались достаточно удаленными от области, в которой находилось электромагнитное поле. Во многих практических задачах часто требуется непосредственно связать величину сторонних электрических токов, являющихся источниками электромагнитного поля, с векторами и в любых точках пространства. Сюда относится, прежде всего, большинство задач из теории излучающих антенн. Другим примером может служить задача о возбуждении объемного резонатора с помощью штыря, щели, электронного пучка и т. д.

С математической точки зрения решение всех указанных задач сводится к решению неоднородной системы уравнений Максвелла, которая может быть записана следующим образом:

.

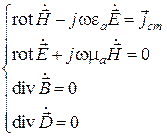Здесь для простоты предполагается, что плотность объемного заряда .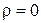

Подчеркнем, что в правой части этой системы записана плотность стороннего электрического тока, являющаяся известной векторной функцией пространственных координат. В этом смысле имеется прямая аналогия между неоднородной задачей электродинамики и задачей о нахождении токов в напряжений в электрической цепи, на которую воздействуют заданные сторонние ЭДС.