Добротность объемных резонаторов

Добротность − одна из общих характеристик, присущих любым колебательным системам независимо от их физической природы. Ее можно определить как величину, пропорциональную числу свободных колебаний, которые успевает совершить система за время переходного процесса вплоть до момента затухания, определяемого любым известным способом, например, по уровню 10% от начальной амплитуды. Конкретно принято определять добротность следующим образом:

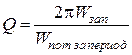
Здесь 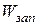− энергия, запасенная в системе, которая вычисляется в какой-либо определенный момент времени; 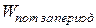− средняя величина энергии потерь. вычисленная за тот период колебаний, в который была найдена 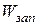. Последнюю из данных характеристик можно выразить через мощность потерь:

,

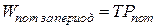откуда

.

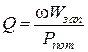Перейдем к конкретному рассмотрению добротности электромагнитных объемных резонаторов. В целях большей общности будем полагать, что резонатор представляет собой замкнутый объем 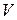, ограниченный поверхностью 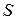. Будем полагать также, что потери энергии в резонаторе связаны лишь с конечной проводимостью материала стенок, что представляет наибольший практический интерес. Проводимость материала стенок будем считать достаточно высокой для того, чтобы можно было применить приближенные граничные условия Леонтовича.

Как показал Максвелл, энергию электромагнитного поля в объеме можно найти, интегрируя по объему квадрат электрического или магнитного векторов: 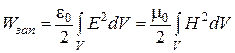. Заметим, что в эту формулу надо подставлять величины или , которые относятся к идеальному резонатору без потерь.

Мощность потерь, приходящаяся на 1 кв. м. поверхности металлических стенок, была определена ранее при расчете затухания в волноводе. Соответствующая формула имеет вид

.

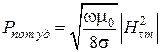Здесь полагаем, что металл не обладает собственными магнитными свойствами, т.е. .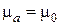

Подставляя окончательно последние формулы в определение добротности, получим

.

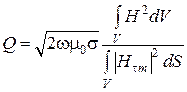При расчете по этой формуле значение частоты нужно полагать равным .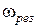

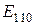Для большинства объемных резонаторов, используемых на практике, в справочной литературе приводятся формулы для расчета добротности. Например, прямоугольный резонатор с типом колебаний или, что то же самое , обладает добротностью, вычисляемой по формуле

Расчет добротности круглого цилиндрического резонатора, работающего на колебании типа 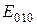, приводит к следующему результату:

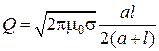
График зависимости добротности от осевого размера 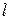, рассчитанный по последней формуле, приведен на рисунке 68. Из графика следует, что в объемных резонаторах без труда может быть достигнута добротность порядка нескольких десятков тысяч, что значительно превышает величины добротностей обычных колебательных контуров, образованных сосредоточенными элементами. Причина этого заключается в том, что объемный резонатор способен накапливать значительное количество электромагнитной энергии при относительно небольших омических потерях. Нарастающий характер кривой на графике объясняется как раз тем, что с ростом 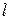объем резонатора, а следовательно, и величина накапливаемой энергии возрастают быстрее, чем мощность потерь, пропорциональная его поверхности.

Рисунок 68 − Добротность объемного резонатора в зависимости от размера

В заключение необходимо сделать два существенных замечания. Во-первых, реально достижимые цифры добротностей, как правило, несколько ниже теоретических, поскольку здесь не учитываются потери в трущихся контактах между боковой поверхностью резонатора и одной из торцевых поверхностей, которую приходится перемещать вдоль оси в целях перестройки резонатора по частоте.

Во-вторых, в приведенных расчетах не учитывается шунтирующее действие внешних цепей, проявляющееся через элементы связи. Поэтому добротность резонатора, найденную описанным способом, принято называть ненагруженной или собственной добротностью в отличие от нагруженной добротности, которая оказывается тем ниже, чем выше коэффициент связи резонатора с внешними цепями.