Круглые объемные резонаторы

Рассмотрим цилиндрический объем, изображенный на рисунке 62, представляющий собой отрезок круглой металлической трубы радиуса 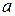, ограниченный с двух сторон проводящими торцевыми поверхностями. Данная система носит название круглого объемного резонатора. Поставим задачу нахождения всей совокупности резонансных частот данного резонатора.

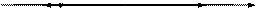
Рисунок 62 − Круглый объемный резонатор

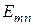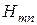Внутри бесконечного круглого волновода могут распространяться волны типа и . Длина волны в волноводе 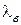связана с длиной волны в свободном пространстве 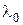при помощи дисперсионного уравнения

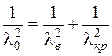
независимо от типа волны. Критические длины волн вычисляются следующим образом:

, .

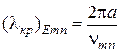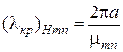Если теперь воспользоваться известным условием резонанса

,

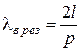то из дисперсионного уравнения вытекают формулы, определяющие резонансные длины волн для любого типа колебаний в круглом резонаторе:

,

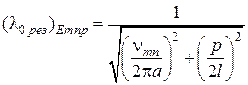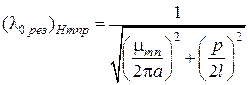
Вопрос о том, имеет ли физический смысл значение , решается таким же образом, как и в случае прямоугольного объемного резонатора. В частности, колебания Е-типа с индексом возможны. Примером здесь может служить часто используемое на практике колебание типа 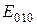, структура поля которого изображена на рисунке 63.

Рисунок 63 − Структура электромагнитного поля колебания типа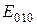

Важным свойством его служит независимость резонансной длины волны от осевого размера 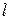, что непосредственно вытекает из структуры поля. Это же подтверждается расчетом по формуле резонансной длины волны:

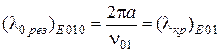
Итак, данная система резонирует на длине волны, которая является критической для порождающего волноводного типа колебаний 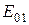. Физически это означает, что стоячие волны в рассматриваемом резонаторе устанавливаются не по оси 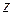, а по радиальной координате .

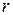Так же, как и в прямоугольном резонаторе, колебания типа 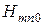в круглом резонаторе существовать не могут.