Объемный резонатор, образованный отрезком прямоугольного волновода

Здесь на простейшем примере будет рассмотрен метод, позволяющий определять резонансную длину волны и структуру электромагнитного поля в объемных резонаторах, представляющих собой отрезки регулярных металлических волноводов. Исходными данными при этом служат характеристики волноводных типов колебаний, распространяющихся в бесконечном волноводе.

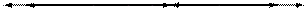
Рисунок 57 − Прямоугольный объемный резонатор

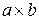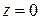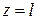Рассмотрим отрезок прямоугольного волновода сечением , ограниченный двумя металлическими торцевыми поверхностями, располагающимися в сечениях и (рисунок 57). Подобная замкнутая металлическая полость представляет собой объемный резонатор. Найдем один из частных видов собственных колебаний данного резонатора руководствуясь следующими соображениями. Пусть по волноводу без торцевых поверхностей распространяется волна основного типа 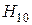, которую условно будем называть падающей волной. Очевидно, что

.

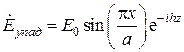Ввиду наличия торцевых поверхностей в системе должна существовать также и отраженная волна, для которой

.

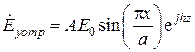Если учесть, что при 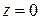суммарное поле 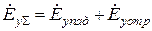должно обратиться в нуль в силу граничных условий на идеальном проводнике, то, как нетрудно видеть, 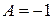. Таким образом,

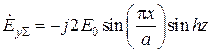
Согласно этой формуле, рассматриваемый электромагнитный процесс представляет собой двумерную стоячую волну, существующую как по оси 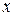, так и по оси 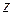. Однако длина стоячей волны по оси 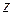пока не определена, поскольку не наложено никаких условий на продольное волновое число 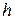. Данные условия естественно вытекают из того, что должно выполняться тождество

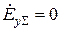при ,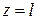

откуда

.

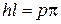Значение продольного волнового числа, удовлетворяющее данному равенству, будем называть резонансным значением

.

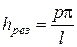Отсюда нетрудно перейти к резонансному значению длины волны в волноводе

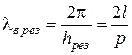
и в свободном пространстве

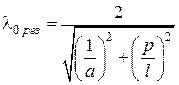
Подведем некоторый итог. Итак, удалось показать, что для прямоугольной металлической полости решения могут существовать не при любой длине волны возбуждающего источника, а лишь в бесконечной последовательности отдельных точек, удовлетворяющих резонансному условию (последнее уравнение). Каждому отдельному значению целочисленного индекса 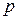соответствует своя величина резонансной длины волны и своя характерная структура электромагнитного поля, представляющая собой тип колебаний прямоугольном объемном резонаторе.

Так же, как и в случае регулярных волноводов, для объемных резонаторов возможно классифицировать типы колебаний. Более подробно этот вопрос будет изучен ниже. Здесь укажем лишь, что исследуемая совокупность типов колебаний может быть обозначена как 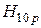.Такая символика показывает, что поле объемного резонатора порождается волноводным типом колебаний 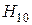, причем вдоль продольной оси 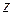укладывается 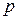стоячих полуволн.

Структуру электромагнитного поля удобно проследить на примере простейшего типа колебаний . Здесь, очевидно,

.

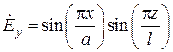(амплитудный множитель для удобства принят равным единице).

Магнитное поле в резонаторе без труда находится на основании второго уравнения Максвелла 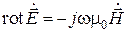, откуда

.

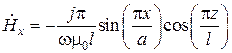Следует обратить внимание на очень важный факт наличия мнимых единиц в амплитудных множителях при составляющих магнитного вектора. Их присутствие говорит о том, что между мгновенными значениями электрического и магнитного полей в резонаторе постоянно существует сдвиг фаз по времени на величину 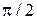. Это является следствием того, что в объемном резонаторе, как и в любой электромагнитной колебательной системе, происходит непрерывный процесс обмена энергий между электрическим и магнитным полями. Так же, как и в обычном колебательном контуре, дважды за период энергия электрического поля переходит в энергию магнитного поля и наоборот. Сказанное иллюстрируется мгновенными картинами распределения электромагнитного поля в объемном резонаторе с колебаниями типа , построенными для различных моментов времени и представленными на рисунке 58.

Отметим также, что вектор Пойнтинга, образованный полями в резонаторе, имеет тождественно равное нулю среднее значение. Это значит, что объемный резонатор, с энергетической точки зрения, подобен колебательному контуру.

Рисунок 58 − Структура электромагнитного поля резонатора в последовательные моменты времени для колебаний типа

Рисунок 59 − Картина поверхностных токов на стенках резонатора

Остановимся, наконец, на важном для практики вопросе о поверхностных токах, протекающих по стенкам резонатора. Так как вектор плотности поверхностного тока на идеально проводнике перпендикулярен тангенциальной составляющей магнитного поля, легко приходим к картине, изображенной на рисунке 59 для некоторого фиксированного момента времени. Здесь токи проводимости, стекающиеся к центру верхней крышки резонатора, замыкаются внутри него посредством токов смещения. Последние, в свою очередь, охватываются кольцевыми линиями магнитного поля в соответствии с законом полного тока.