ИЗУЧЕНИЕ ЗАВИСИМОСТИ СПЕКТРОВ ПРЯМОУГОЛЬНОГО И СИНУСОИДАЛЬНОГО МОДУЛИРОВАННОГО СИГНАЛОВ ОТ ИХ ПАРАМЕТРОВ

Сигнал есть физический процесс, который несет в себе информацию. Информация, содержащаяся в сигнале, выражается зависимостью от времени какого-либо параметра сигнала S(t). Из математики известно, что любую функцию S(t), кусочно-гладкую на интервале от t=a до t=b и ограниченную по норме

,

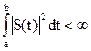можно разложить в ряд по полному набору ортогональных функций j_n(t):

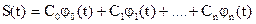. (1)

Для периодических функций в качестве интервала [a,b] удобно брать период [-T/2,T/2]. Вид разложения (1) зависит не только от вида выбранных базисных функций j_n(t), но и от способа выбора коэффициентов разложения C_n. Если коэффициенты C_n определяются по формуле

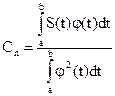, (2)

то ряд (1) называется обобщенным рядом Фурье, который при фиксированном числе слагаемых ряда обеспечивает минимум среднеквадратичной ошибки разложения:

.

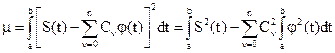В качестве функций j_n(t) в радиотехнике используют тригонометрические функции sin(wt), cos(wt). Это объясняется рядом причин:

а) гармоническое колебание является собственным видом колебаний линейных систем с постоянными параметрами (колебательные контуры и др.);

б) гармоническое колебание является единственной функцией времени, сохранявшей свою форму при прохождении через любую линейную систему с постоянными параметрами, а изменяться может лишь амплитуда и фаза колебаний;

в) гармонические функции sin(wt), cos(wt) являются ортогональными, они просты и определены при всех значениях t;

г) для гармонических функций и их комплексного аналога разработан мощный математический аппарат, упрощающий анализ, найдены спектры множества форм сигналов и т. д.

Вид Фурье-разложения сигнала S(t) c периодом Т по гармоническим функциям следующий:

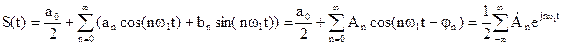, (3)

где согласно (2) коэффициенты разложения равны:

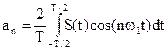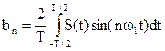; , (4)

где , ,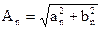

, .

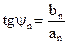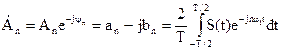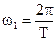Таким образом, спектр периодической функции является линейчатым или дискретным, т. к. состоит из отдельных гармоник, y_n — фаза гармоник. Важно подчеркнуть, что Фурье-разложение (3) не есть чисто математическая абстракция и его можно осуществить реально. Для этого нужно сложить достаточно большое число гармонических сигналов с частотами и амплитудами необходимых гармоник разложения, в результате получим исходный сигнал S(t).

Таким образом, можно считать, что сигнал S(t) действительно состоит из суммы гармонических сигналов, каждый из которых можно выделить из сигнала S(t), например, с помощью фильтров.

Рассмотрим пример разложения сигнала, состоящего из последовательности униполярных прямоугольных импульсов амплитудой Е, длительностью импульса t и периодом следования Т (рис.1).

Спектр такого сигнала согласно (3) и (4) можно представить в следующем виде:

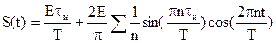, (5)

где амплитуда n-гармоники

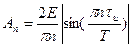, (6)

а ее частота

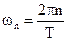. (7)

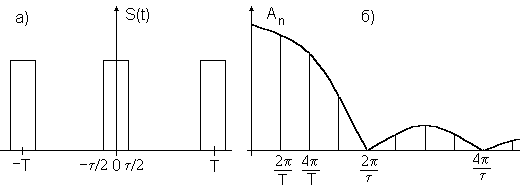
Рис. 1. Последовательность униполярных прямоугольных импульсов (а)

и ее спектр (б)

Как следует из (6), амплитуда гармоник, уменьшаясь с увеличением номера как 1/n, одновременно изменяется по закону синуса. Подставляя значение n из (7) в (6), получим, что огибающая амплитуд гармоник, определяющая ширину спектра, изменяется по закону:

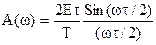(8)

и на частотах, кратных величине 2p/t, обращается в ноль. Таким образом, ширина спектра определяется только длительностью импульса.

Расстояние между соседними гармониками w₁=2p/T обратно пропорционально периоду следования импульсов, и если этот период неограниченно увеличивать (как бы переходя к одиночному импульсу, удаляя остальные в бесконечность), то расстояние между гармониками стремится к нулю, т. е. будет происходить переход от дискретного спектра к сплошному. При этом амплитуда гармоник вследствие увеличения n будет стремиться к нулю и вместо нее пользуются другой характеристикой S(w) — спектральной плотностью одиночного сигнала, причем выполняется соотношение:

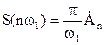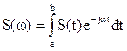, . (9)

В частном случае одиночного прямоугольного импульса длительностью t

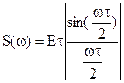, (10)

т. е. принимает форму огибающей линейчатого спектра последовательности прямоугольных импульсов и отличается только масштабом: p/w₁=Т/2.

В качестве второго примера рассмотрим спектр амплитудно-модулированного сигнала при модулирующей функции в виде косинуса (так называемая одноканальная модуляция):

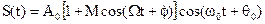. (11)

Раскрывая квадратные скобки и производя тригонометрические преобразования, получим:

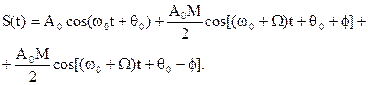(12)

Таким образом, спектр такого колебания состоит из трех гармоник: несущей частоты и двух боковых частот, сдвинутых относительно несущей на значение частоты модуляции W.

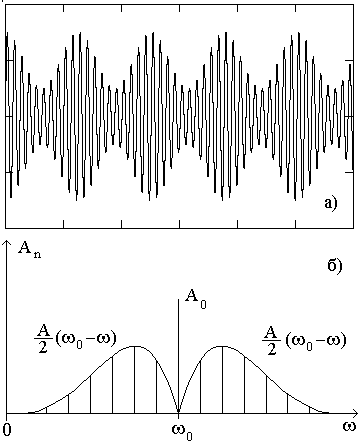
Рис. 2. Амплитудно-модулированный синусоидальный сигнал (а),

спектр амплитудно-модулированного сигнала (б)

Амплитуды боковых частот пропорциональны глубине амплитудной модуляции М и при М=1 составляют половину амплитуды несущей. В общем случае произвольной модулирующей функции А(t) спектр амплитудно-модулированного сигнала будет состоять на несущей частоты и расположенных по обе стороны от нее спектров модулирующей функции A(t) (рис. 2).