СИЛА ДАВЛЕНИЯ В ЖИДКОСТИ. ДАВЛЕНИЕ
Гидростатика изучает жидкости, которые находят- ся в состоянии равновесия.
Жидкости имеют особые механические свойства:
—  малая сжимаемость (жидкость практически сохраняет свой объём даже при больших внешних силах давления),
малая сжимаемость (жидкость практически сохраняет свой объём даже при больших внешних силах давления),
— в земных условиях жидкость принимает форму того сосуда, в котором она находится.
В жидкости действуют силы упругости, которые направлены перпендикулярно к любой твердой поверхности или границе. Эти силы называются с и л а м и д а в л е н и я.
Силы давления распределяются по поверхности, на которую они действуют (рис. 94).
Д а в л е н и е м называется физическая величина, равная отношению модуля силы давления к площади поверхности, на которую сила давления действует:
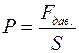 , (V.1)
, (V.1)
где Р — давление,
Fдав. — сила давления,
S — площадь поверхности.
Единица давления в СИ — 1 паскаль:
[Р] = 1 Па = 1 Н/м2.
Единица давления в системе СГС — 1 дин/см2.
На практике часто используют внесистемные единицы давления:
— 1 миллиметр ртутного столба,
1 мм рт. cт. » 133 Па;
— 1 физическая атмосфера (обозначается 1 атм),
1 атм = 760 мм рт. ст.= 1,013× 105 Па;
— 1 техническая атмосфера (обозначается 1 ат),
1 ат = 1 кгс/см2 = 9,8×104 Па.
| гидростатика | hydrostatics | hydrostatique | hydrostática |
| несжимаемость | incompressibility | incompressibilité | incompresibleción |
| текучесть | fluidity | fluidité | fluidez |
| давление | pressure | pression | presión |
| ртутный столб | colomn of mercury | colonnе de mercure | mercurio columna |
| производить | produce | produire | producir |
2. ЗАКОН ПАСКАЛЯ
Если жидкость находится в равновесии и к повер- хности жидкости приложены внешние силы, то выполняется закон Паскаля: давление, которое производят внешние силы на поверхность жидкости, передаётся во все точки жидкости без изменения.
Рассмотрим гидравлическую машину, действие которой основано на законе Паскаля.
Гидравлическая машина состоит из двух цилинд- ров, которые соединены между собой (рис. 95). В цилиндрах под поршнями находится жидкость (масло). Площадь поршня в первом цилиндре — S1, площадь поршня во втором цилиндре — S2 (S1 < S2). Пусть на малый поршень 1 действует сила 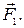 По закону Паскаля давление, которое создаёт эта сила
По закону Паскаля давление, которое создаёт эта сила  жидкость передаёт без изменения в цилиндр 2:
жидкость передаёт без изменения в цилиндр 2:
P1 = P2.
Давление жидкости в цилиндре 2 можно выразить через силу F2, с которой жидкость действует на поршень 2, и площадь этого поршня S2:
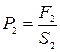 .
.

Таким образом,

или
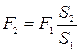 (V. 2)
(V. 2)
Сила F2 больше силы F1 во столько раз, во сколько раз площадь поршня S2 больше площади поршня S1.
Если под действием силы F1 поршень 1 перемещается на расстояние ℓ1, то поршень 2 перемещается на расстояние ℓ2. Из условия несжимаемости жидкости следует
V1 = V2 Þ S 1 × ℓ 1 = S2 × ℓ или 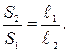
Подставляем это соотношение в формулу (V. 2) и находим, что F 1 × ℓ 1 = F 2 × ℓ , т. е. A 1 = A 2.
С д е л а е м в ы в о д: гидравлическая машина даёт выигрыш в силе, но не даёт выигрыша в работе.
Гидравлическая машина широко используется в технике для получения и передачи на расстояние больших сил (гидравлический пресс, гидравлический домкрат, гидравлическая передача).
3. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ

 Г и д р о с т а т и ч е с к и м называется давление, которое создаёт сила тяжести, действующая на жидкости.
Г и д р о с т а т и ч е с к и м называется давление, которое создаёт сила тяжести, действующая на жидкости.
Пусть масса жидкости в сосуде (рис. 96) равна


 т = rж × S × h, (V.3)
т = rж × S × h, (V.3)
|
|
|





 где rж — плотность жидкости;
где rж — плотность жидкости;
|




 h — высота столба жидкости в сосуде;
h — высота столба жидкости в сосуде;
 S — площадь основания сосуда.
S — площадь основания сосуда.
|
|

|






 Сила гидростатического давления жидкости на дно сосуда, которая находится в равновесии, равна Fдав. = mg, или Fдав. = rж × S × h × g.
Сила гидростатического давления жидкости на дно сосуда, которая находится в равновесии, равна Fдав. = mg, или Fдав. = rж × S × h × g.



 Подставляя это значение силы давления Fдав. в формулу (V.1), получим формулу гидростатического давления жидкости на дно сосуда
Подставляя это значение силы давления Fдав. в формулу (V.1), получим формулу гидростатического давления жидкости на дно сосуда
|
 Р = rж × g × h. (V.4)
Р = rж × g × h. (V.4)
Давление жидкости на дно сосуда не зависит от формы сосуда, а зависит только от высоты поверхности жидкости над дном (т. е. от высоты столба жидкости).
По формуле (V.4) гидростатическое давление на любом уровне жидкости (на любой горизонтальной поверхности) равно (см. рис. 96):
— на уровне ВВ' Þ Р ВВ` = rж × g × h1,
где h1 — высота поверхности жидкости в сосуде отно- сительно уровня ВВ' (т.е. глубина уровня жидкости ВВ');
— на уровне СС' Þ Р CC` = rж × g × h2,
где h2 — высота поверхности жидкости в сосуде отно- сительно уровня СС' (т.е. глубина уровня жидкости СС').
Гидростатическое давление в однородной жидкос- ти увеличивается пропорционально глубине: РCC`> РBB`.
Из закона Паскаля и формулы (V.4) следует условие равновесия жидкости: давление на любом горизонтальном уровне жидкости, которая находится в равновесии, одинаково во всех точках на этом уровне.
Например (см. рис. 96):
РВ = Р В` так как hB = hB` = h1,
РС = РС`, так как hС = hС` = h2,
но РВ ≠ РС и Р В` ≠РС`;
— если на открытую поверхность жидкости действует внешнее давление (например,атмосферное давление Рат), то полное давление в любой точке жидкости равно
Р = Рат + rж × g × h, (V.5)
где Рат — атмосферное давление;
rж×g × h — гидростатическое давление столба жидкости
высотой h над уровнем, которому принадлежит данная точка.
4. СООБЩАЮЩИЕСЯ СОСУДЫ
С о о б щ а ю щ и м и с я с о с у д а м и называются два или несколько сосудов, которые соединяются друг с другом (рис. 97).
С в о б о д н о й п о в е р х н о с т ь ю жидкости называется поверхность жидкости, которая не соприкасается со стенками сосуда.
Из закона Паскаля и формулы (V.4) следует, что свободная поверхность однородной жидкости (r1 = r2) в состоянии равновесия в сообщающихся сосудах устанавливается на одном горизонтальном
уровне (см. рис. 97).
 Если в сообщающихся сосудах находятся несмешивающиеся жидкости с разными плотностями (r1 ¹ r2), то свободные поверхности жидкостей в разных сосудах могут находиться на разных
Если в сообщающихся сосудах находятся несмешивающиеся жидкости с разными плотностями (r1 ¹ r2), то свободные поверхности жидкостей в разных сосудах могут находиться на разных
уровнях (см. рис. 98):
 (V.6)
(V.6)
5. ЗАКОН АРХИМЕДА
Определим силу F¢, с которой тело растягивает пружину, если:
— тело находится в воздухе 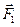 (рис. 99, а).
(рис. 99, а).
— тело находится в жидкости 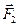 (рис. 99, б).
(рис. 99, б).
В первом случае эта сила равна
F1¢ = mg. (V.7)
Во втором случае сила, с которой тело растягивает пружину, уменьшается:
F¢2 < F¢1

а б
С д е л а е м в ы в о д: на тело со стороны жидкости действует сила, направленная вертикально вверх, которая выталкивает тело из жидкости. Эту силу называют в ы т а л к и в а ю щ е й с и л о й 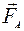 или силой Архимеда (см. рис. 99, б).
или силой Архимеда (см. рис. 99, б).
Таким образом,
F¢2 = F¢1 - FA . (V.8)
Вычислим величину выталкивающей силы, с которой жидкость плотностью rж действует на тело (параллелепипед) высотой Н и площадью основания S (рис. 100). Глубина погружения верхнего основания h, глубина погружения нижнего основания h + H. На тело со всех сторон действуют силы давления. Силы давления на боковые поверхности параллелепипеда уравновешивают друг друга:
Fдав. 3 = Fдав. 4; Fдав. 5 = Fдав. 6.
Сила давления на нижнее основание больше, чем на верхнее основание
Fдав. 2 > Fдав. 1 [см. формулу (V.4)].
Таким образом, равнодействующая всех сил давления жидкости на твердое тело — выталкивающая сила — направлена вертикально вверх и равна
FА = Fдав. 2 - Fдав.1,
где
rж × g × h1× S + Рат × S = (Р1+ Рат)S = Fдав.,1
rж × g × ( h + Н) × S + Рат× S = (Р2 + Рат)S = Fдав.,2.
Тогда
FА = rж × g × Н × S,
где Н × S― объём жидкости, вытесненной телом (Vвыт.ж.).

Объём жидкости, вытесненной телом (Vвыт.ж.) равен:
―объёму тела, если всё тело находится в жидкости (рис. 101, а):
Vвыт.ж. = Vтела = V1 + V2;
— объёму той части тела, которая находится в жидкости (рис. 101, б ).
Vвыт. ж. = V2.

а б
Поэтому
FА = rж × g × Vвыт.ж. = Рвыт. ж.. (V.9)
Формула (V.9) — это математическое выражение закона Архимеда:
На тело, погружённое в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости, вытесненной телом.
Выталкивающая сила приложена в центре объёма жидкости, вытесненного телом.
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. В чём различие понятий: сила давления и давление?
2. Какое соотношение между единицами давления?
3. Какой закон лежит в основе действия гидравлической машины?
4. Что является причиной гидростатического давления?
Основные формулы гидростатики
Давление
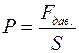 Закон Паскаля:
формулы гидравлической машины
Закон Паскаля:
формулы гидравлической машины
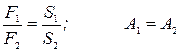 гидростатическое давление
Р = rж × g × h
Закон Архимеда:
FА = rж. × g × Vвыт.ж. = Рвыт. ж.
гидростатическое давление
Р = rж × g × h
Закон Архимеда:
FА = rж. × g × Vвыт.ж. = Рвыт. ж.
|
| гидравлический | hydraulic | hydrolique | hydráulica |
| поршень | piston | piston | pistón |
| пресс | press | press | prensa |
| глубина | depth | profondeur | profundidad |
| выталкивающая сила | up thrust force | force de poussée | fuerza de empuje |
| плавать | float | flotter | flotar |
| плавание | floation | flottement | natación |
| всплывать | come to surface | émerger | subir a la superficie |
| тонуть | sink | s`enfoncer | hundirse |
VI. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
В природе часто встречается движение, которое повторяется во времени. Например, движение точки колеса при равномерном вращении, движение точек натянутой струны, движение маятника механических часов (рис. 102). Это примеры периодического движения.
а б в
Рис. 102
Периодическим называется такое движение, отдельные этапы которого точно повторяются через определенный интервал времени.
Частный случай периодического движения — это колебательное движение. Такое движение может совершать тело или система тел, которые имеют положение устойчивого равновесия.
К о л е б а т е л ь н о е д в и ж е н и е — это такое периодическое движение, при котором тело или система тел отклоняются от некоторого положения равновесия то в одну, то в другую сторону.
Среди примеров, показанных на рис. 102, колебательное движение (или просто колебания) совершают натянутая струна и маятник часов (рис. 102, б, в).
Шарик на вогнутой поверхности также будет совершать колебательное движение относительно положения устойчивого равновесия, если в начальный момент он будет выведен из положения равновесия и предоставлен самому себе (см. рис. 88).
Колебания системы тел могут быть свободными и вынужденными.
С в о б о д н ы м и, или с о б с т в е н н ы м и, называются колебания системы тел, на которую не действуют периодические внешние силы.
Свободные колебания совершают натянутая струна и шарик на вогнутой поверхности, если их отклонить от положения равновесия и предоставить самим себе.
В ы н у ж д е н н ы м и называются колебания системы тел, на которую действует периодическая внешняя сила.
1. ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
П е р и о д (обозначается Т) — это время одного полного колебания (одного цикла колебания). В системах единиц СИ и СГС период измеряется в секундах.
Ч а с т о т а (обозначается f ) — это величина, обратная периоду и равная числу колебаний за одну секунду:

Единица измерения частоты колебаний в системах СИ и СГС называется герц:
[ f ] = 1 Гц = 1 с-1.
При частоте в один герц тело или система тел совершают одно колебание за одну секунду.
На практике часто используют единицы измерения частоты:
1 килогерц = 1 кГц = 103Гц,
1 мегагерц = 1 мГц = 106 Гц.
Если система тел совершает свободные (собственные) колебания, то частота таких колебаний называется собственной частотой.
Смещение (обозначается х) — это величина отклонения тела или системы тел от положения устойчивого равновесия. Наиболее часто смещение измеряется в единицах длины:
в системе СИ [х] = 1 м,
в системе СГС [х] = 1 см.
Функция зависимости смещения от времени x (t) полностью описывает данное колебательное движение.
Рассмотрим наиболее простой вид колебаний — гармонические колебания.
Г а р м о н и ч е с к и м и называются такие колебания, при которых смещение изменяется со временем по закону синуса или косинуса:
х (t) = А × sin (wt + j0). (VI. 1)
В формуле (VI. 1) содержатся следующие характеристики гармонических колебаний.
А м п л и т у д а:
(обозначается А) — это величина максимального смещения; измеряется в единицах длины.
Ц и к л и ч е с к а я ч а с т о т а:
(обозначается w) — греческая буква «омега») — это величина, связанная с частотой и периодом соотношением
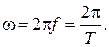
Единица измерения циклической частоты — радиан в секунду

Ф а з а к о л е б а н и я:
(обозначается j — греческая буква «фи»)
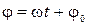
Н а ч а л ь н а я ф а з а:
(обозначается j0) — это фаза колебания в момент времени t = 0.
Если начальная фаза равна нулю j0 = 0, то в начальный момент времени t = 0 смещение тела равно нулю х = 0, т. е. тело находится в точке положения равновесия.
Фаза и начальная фаза измеряются в радианной мере угла.
Некоторые перечисленные характеристики колебаний удобно показать на графике зависимости смещения от фазы. Пусть у нас есть две системы тел, которые совершают гармонические колебания с одинаковой амплитудой и частотой, но с разными начальными фазами: для первой колебательной системы начальная фаза равна нулю:
х1 = х1(j) = А × sin wt,
a для второй системы начальная фаза отлична от нуля
х2= х2(j)= А × sin (wt + j0).
Пусть в данном случае аргументом функции смещения будет фаза первой колебательной системы j = wt. На рис. 103 показаны графики этих двух колебаний — две синусоиды.
Рассмотрим, как параметры колебаний связаны с геометрическими характеристиками графиков на рис. 103.

Для колебательного движения х1(j), например в точке n, смещение х n равно длине отрезка ND, фаза j n равна длине отрезка фазовой оси ОD. Разность фаз между точками с одинаковым смещением М и N, равная 2p, соответствует периоду колебания Т. Максимальное смещение равно амплитуде А.
На рис. 103 видно также, что синусоида х1(j) начинается в точке х1= 0 (в точке положения равнове- сия) при j = 0, что соответствует начальному моменту времени t = 0. Синусоида х2(j) приходит в положение х = 0 только через некоторое время, которому соответ- ствует отрезок фазовой оси ОС. Длина этого отрезка по модулю равна начальной фазе: ОС = j0.
Если смещение точки при гармонических колебаниях изменяется по закону синуса (VI. 1), то скорость движения точки, которая совершает колебательное движение, изменяется по закону:
υх (t) = w× А × cos (wt + j0), (VI. 2)
а ускорение
ах (t) = - w2× А × sin (wt + j0). (VI. 3)
| !!! ЗАПОМНИТЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ: х ― смещение А ― амплитуда Т ― период j = (wt + j0) ― фаза колебания f ― частотаj0 ― начальная фаза w ― циклическая частота |
??? ОТВЕТЬТЕ НА ВОПРОСЫ:
1. В чём различие периодического и колебательного движений?
2. Что такое собственная частота колебаний?
3 Какими характеристиками полностью определяется гармоническое колебание?
4. Что есть общего и различного в параметрах колебаний: а) смещение и амплитуда? б) частота и циклическая частота? в) фаза и начальная фаза?
5. Как выразить фазу через период колебаний?
6. Как изменятся параметры гармонических колеба- ний, если уравнение (VI.1) записать не через синус, а через косинус?
| колебания | oscillations | oscillations | oscilaciónes |
| маятник | pendulum | pendule | péndulo |
| шнур | |||
| свободные (собственные) колебания | free (natural) oscillations | oscillations libres (propres) | oscilaciónes libres |
| вынужденные колебания | forced oscillations | oscillations forcées | oscilaciónes forzadas |
| параметр | parameter | paramètre | parámetro |
| период | period | périod | periodo |
| частота | frequency | fréquence | frecuencia |
| амплитуда | amplitude | amplitude | amplituda |
| гармонические колебания | harmonic oscillations | oscillations harmoniques | oscilaciónes harmónicas |
| циклическая частота | circular frequency | fréquence cyclique | frecuencia cíclica |
| фаза | phase | phase | fase |
| радианная мера угла | radian measure of angle | mesure d`un angle en radiane | medida en radianes del ángulo |
Дата добавления: 2015-09-28; просмотров: 957;
