Дифференциальные уравнения равновесия жидкости

Возьмём в покоящейся жидкости точку D с координатами x,y,z и выделим при ней элементарный объём в виде прямоугольного параллелепипеда со сторонами dx, dy, dz (рис. 2.3). Его объем равен 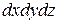, а масса − .

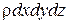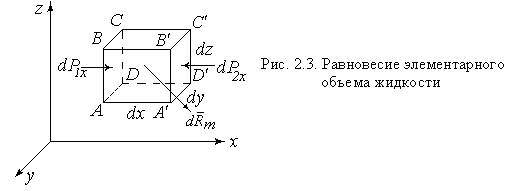
На выделенный элемент действует массовая сила 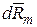и поверхностные

силы давления, направленные нормально к граням внутрь объема.

Составим уравнение равновесия объема в проекции на ось х. Будем считать, что по бесконечно малой площадке давление распределено равномерно и равно среднему давлению (давлению в центре грани). На грань 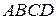действует давление p и вызванная им сила 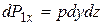. На грань 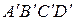действует давление 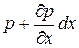. Оно создает силу 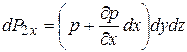, направленную противоположно оси x.

Единичная массовая сила, действующая в жидкости, имеет составляющие X,Y,Z. Проекция массовой силы 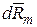на ось х будет равна .

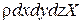Итак, уравнение равновесия в проекции на ось х запишется в виде:

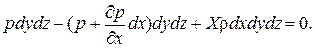(2.3)

Открыв скобки, сократив на не равное нулю произведение 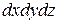и разделив на ρ, получим 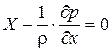. Аналогично выглядят проекции уравнения равновесия на другие оси. В итоге получим систему дифференциальных уравнений равновесия (уравнений Эйлера), имеющую вид:

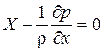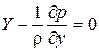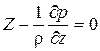; ; . (2.4)

Для решения этой системы сведём её к одному уравнению. Для этого умножим первое на dx, второе на dy, третье на dz и сложим все три уравнения. Получим : 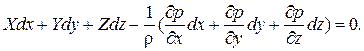(2.5)

Трёхчлен в скобках – полный дифференциал давления dp. В итоге получим:

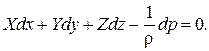(2.6)

Это уравнение также является дифференциальным уравнением равновесия. Оно может быть решено, если известны проекции единичных массовых сил X, Y, Z.

Запишем последнее уравнение в виде 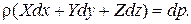Поскольку жидкость рассматриваем как несжимаемую (ρ=const), то уравнение имеет смысл, если выражение в скобках представляет собой полный дифференциал,

как и правая часть. Для этого необходимо, чтобы существовала некоторая функция U(x,y,z), частные производные от которой равнялись бы проекциям X,Y,Z , то - есть должны существовать равенства:

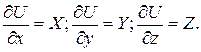(2.7)

Функцию U можно назвать силовой или потенциальной. Так как массовые силы пропорциональны создаваемым ими ускорениям X,Y,Z, то их называют силами, имеющими потенциал.

Введем понятие поверхности равного давления. Это поверхность,

проведенная в жидкости так, что на ней давление постоянно (p = const, dp=0).

Уравнение равновесия будет для нее иметь вид:

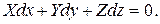(2.8)

Это и есть уравнение поверхности равного давления. Из аналитической геометрии известно, что это – условие перпендикулярности двух векторов с проекциями dx,dy,dz и X,Y,Z. Поскольку dx,dy,dz − проекции отрезка, лежащего на поверхности равного давления, а X,Y,Z − проекции результирующей единичной массовой силы, то можно сделать вывод: поверхность равного давления перпендикулярна направлению результирующего ускорения от массовых сил, действующих в жидкости.

Частным случаем поверхности равного давления является свободная поверхность, отделяющая жидкость от окружающей среды − на ней давление равно давлению окружающей среды.