Выбор теоретического закона распределения ресурсов. При подборе теоретического закона распределения необходимо знать, что опытная исходная информация об изменениях случайной величины обычно представляет собой
При подборе теоретического закона распределения необходимо знать, что опытная исходная информация об изменениях случайной величины обычно представляет собой некоторую выборку из всей генеральной совокупности возможных значений случайной величины. Поэтому статистический ряд распределения и кривая накопленных опытных вероятностей содержат ошибки исходной информации.
Теоретический закон распределения известен, если определены теоретическая дифференциальная f(T) и теоретическая интегральная F(T) функции распределения. Применительно к надежности сельскохозяйственной техники используются, главным образом, ЗНР и ЗРВ.
Предварительный выбор ТЗР осуществляется по величине коэффициента вариации (V). Если V<0,3 то распределение подчиняется ЗНР, если V>0,5 – ЗРВ. Если V лежит в интервале от 0,3 до 0,5, то выбирается тот закон, который лучше совпадает с опытной информацией. Точность совпадения оценивается по критерию согласия.
В нашем случае коэффициент вариации V=0,33, поэтому подходят как ЗНР, так и ЗРВ. Для окончательного решения о выборе ТЗР необходимо рассчитать дифференциальную f(T) и интегральную F(T) функции распределения износа детали по ЗНР и ЗРВ, а затем с помощью критерия согласия выбрать ТЗР.
Дифференциальная функция ЗНР определяется по формуле:
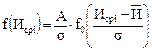 , (50)
, (50)
где А – протяженность интервала, мм;
s – среднее квадратическое отклонение, мм;
Исрi – значение износа в середине i-го интервала, мм;
f0 – центрированная дифференциальная функция (табулирована, ее значение определяется по таблице Б2 приложения Б).
Необходимо учитывать, что:
f0(-И)=f0(И) (51)
Расчет ведется для каждого интервала.
В нашем примере для первого интервала:
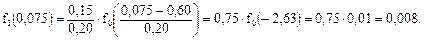
Значение f0(-2,63) находится по таблице Б2 приложения Б, для чего в первой вертикальной колонке находим строку 2,6, а в третьей вертикальной колонке 3, получаем f0=0,01.
Для второго интервала:
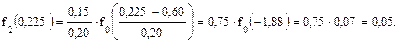
Аналогичные расчеты проводят и для остальных интервалов:
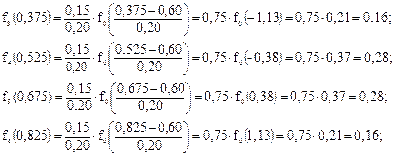

Полученные данные заносят в таблицу 10.
Значение интегральной функции F(Иki) ЗНР в конце i-го интервала определяется по формуле:
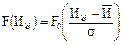 , (52)
, (52)
где F0 – центрированная интегральная функция (табулирована, ее значение определяется по таблице Б3 приложения Б);
Икi – значение износа в конце i-го интервала статистического ряда, мм;
 – среднее значение износа, мм;
– среднее значение износа, мм;
s – среднее квадратическое отклонение, мм.
Необходимо помнить, что:
F0(-И)=1-F0(+И). (53)
Расчет ведется для каждого интервала.
Для нашего примера конец первого интервала Икi=0,15 мм
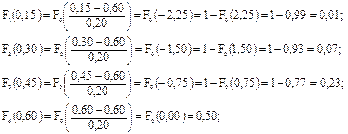
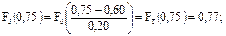
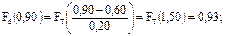
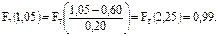
Полученные значения интегральных функций записывают в таблицу 10.
Дифференциальная функция ЗРВ определяется по формуле:
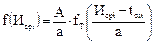 , (54)
, (54)
где А – протяженность интервала, мм;
а – параметр ЗРВ, мм;
tсм – смещение начала рассеивания, мм;
fТ – центрированная дифференциальная функция (табулирована и ее значение определяют по таблице Б5 приложения Б).
Параметр ЗРВ определяется по формуле:
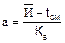 . (55)
. (55)
Коэффициенты ЗРВ (Кв, b, Sв) в зависимости от коэффициента вариации V определяют по таблице Б4 приложения Б.
В нашем случае V=0,33.
Следовательно: b=3,34; Кв=0,898; Sв=0,067.
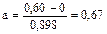 .
.
Расчет f(Исрi) для ЗРВ ведется для каждого интервала и полученные данные также заносят в таблицу 3.
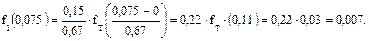
Значения дифференциальной функции 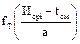 определяют при необходимости с использованием двойного интерполирования по b и
определяют при необходимости с использованием двойного интерполирования по b и 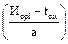 .
.
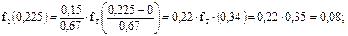

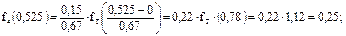

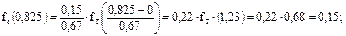
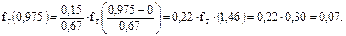
Интегральная функция ЗРВ определяется по формуле:

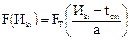 , (56)
, (56)
где F(Иki) – интегральная функция ЗРВ в конце i-го интервала;
F(T) – табулированное значение интегральной функции (см. таблицу Б6 приложения Б);
tсм – смещение начала рассеивания;
а – параметр ЗРВ.
Для нашего примера:
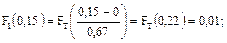
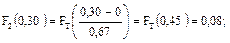
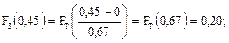
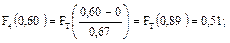
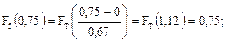
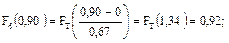

Полученные расчетным путем значения для функций ЗНР и ЗРВ заносят в таблицу 10.
Окончательный выбор ТЗР износов выполняют с помощью критерия согласия. Применительно к показателям надежности сельскохозяйственной техники чаще всего используют критерий Пирсона (χ2) и критерий Колмогорова ( 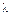 ). По величине критерия согласия можно определить вероятность совпадения опытных и теоретических законов и на этом основании принять или отбросить выбранный теоретический закон распределения, или обоснованно выбрать один теоретический закон из двух или нескольких.
). По величине критерия согласия можно определить вероятность совпадения опытных и теоретических законов и на этом основании принять или отбросить выбранный теоретический закон распределения, или обоснованно выбрать один теоретический закон из двух или нескольких.
Таблица 10 – Выбор ТЗР износов шлицев первичного вала
| Интервал, мото-ч. | 0– 0,15 | 0,15–0,30 | 0,30–0,45 | 0,45–0,60 | 0,60–0,75 | 0,75– 0,90 | 0,90– 1,05 | |
| Середина интервала, Исрi | 0,075 | 0,225 | 0,375 | 0,525 | 0,675 | 0,825 | 0,975 | |
| Конец интервала, мм | 0,15 | 0,30 | 0,45 | 0,60 | 0,75 | 0,90 | 1,05 | |
Накопленная опытная вероятность, 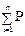 i i
| 0,04 | 0,10 | 0,22 | 0,46 | 0,84 | 0,96 | 1,00 | |
| ЗНР | 
| 0,008 | 0,05 | 0,16 | 0,28 | 0,28 | 0,16 | 0,05 |
| F(Иki) | 0,01 | 0,07 | 0,23 | 0,50 | 0,77 | 0,93 | 0,99 | |
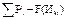
| 0,03 | 0,03 | 0,01 | 0,04 | 0,07 | 0,03 | 0,01 | |
| ЗРВ | 
| 0,007 | 0,08 | 0,17 | 0,25 | 0,24 | 0,15 | 0,07 |
| F(Иki) | 0,01 | 0,08 | 0,20 | 0,51 | 0,75 | 0,92 | 0,99 | |

| 0,03 | 0,02 | 0,02 | 0,05 | 0,09 | 0,04 | 0,01 |
Следует помнить, что критической вероятностью совпадения принято считать Р=10%. Если Р<10%, то выбранный для выравнивания опытной информации ТЗР следует считать недействительным.
Критерий согласия Колмогорова определяют по формуле:
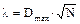 , (57)
, (57)
где 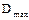 – максимальная абсолютная разность между накопленной опытной вероятностью и теоретической интегральной функцией распределения, т.е.:
– максимальная абсолютная разность между накопленной опытной вероятностью и теоретической интегральной функцией распределения, т.е.:
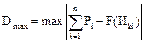 , (58)
, (58)
N – общее количество информации по износам.
Определим разность между накопленной опытной вероятностью и теоретической интегральной функцией распределения по интервалам для ЗНР и ЗРВ.
Для ЗНР:
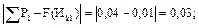

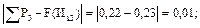
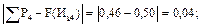
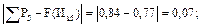

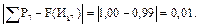
Для ЗРВ:
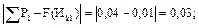
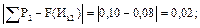
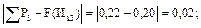



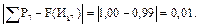
Полученные данные заносят в таблицу 10.
Анализируя полученные данные, видно, что для ЗНР 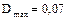 , а для ЗРВ
, а для ЗРВ 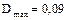 . Тогда расчетное значение критерия согласия Колмогорова будет равно:
. Тогда расчетное значение критерия согласия Колмогорова будет равно:
для ЗНР:
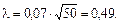
для ЗРВ:

По таблице Б14 приложения Б определим вероятность совпадения 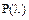 теоретических законов с опытным распределением:
теоретических законов с опытным распределением:
Для ЗНР: 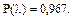
Для ЗРВ: 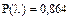 при
при 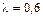 , а с учетом интерполяции, т.е. при
, а с учетом интерполяции, т.е. при 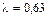
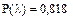 .
.
Следовательно, для выравнивания опытной информации ЗНР подходит лучше, чем ЗРВ (т.к. 0,967>0,818). Выбрав окончательно в качестве теоретического закона ЗНР, наносим на график значения 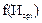 по серединам интервалов и F(Иki) по концам интервалов, которые будут теоретическими дифференциальной и интегральной кривыми распределения износов (см. рисунок 6).
по серединам интервалов и F(Иki) по концам интервалов, которые будут теоретическими дифференциальной и интегральной кривыми распределения износов (см. рисунок 6).
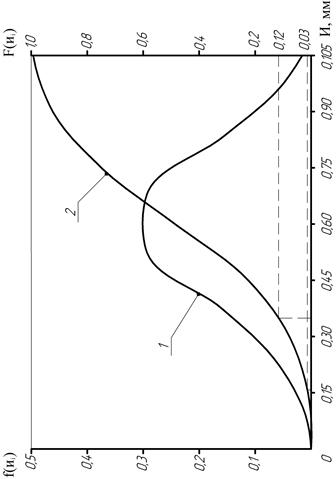
| Рисунок 6 – Теоретическая дифференциальная (1) и теоретическая интегральная (2) кривые распределения износов шлицев |
Дата добавления: 2015-10-19; просмотров: 1393;
