Значения накопленных опытных вероятностей (частостей)
Значения накопленных вероятностей или частостей (последняя строка ряда) определяют суммированием вероятностей по интервалам.
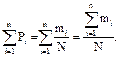 (45)
(45)
Для нашего примера:
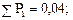
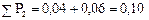 ;
;
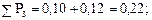
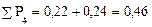
и т.д. по другим интервалам.
Таблица 9 – Статистический ряд распределения износов шлицев первичного вала
| Интервал, мото-ч. | 0– 0,15 | 0,15–0,30 | 0,30–0,45 | 0,45–0,60 | 0,60–0,75 | 0,75–0,90 | 0,90–1,05 |
| Середина интервала, Исрi | 0,075 | 0,225 | 0,375 | 0,525 | 0,675 | 0,825 | 0,975 |
| Частота, mi | |||||||
| Опытная вероятность, Рi | 0,04 | 0,06 | 0,12 | 0,24 | 0,38 | 0,12 | 0,04 |
Накопленная опытная вероятность, 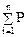 i i
| 0,04 | 0,10 | 0,22 | 0,46 | 0,84 | 0,96 | 1,00 |
2.3.3 Определение числовых характеристик
Основными числовыми характеристиками распределения случайной величины являются: среднее значение, среднее квадратическое отклонение и коэффициент вариации.
Среднее квадратическое отклонение представляет собой абсолютную меру, а коэффициент вариации – относительную меру рассеивания случайной величины. При объеме выборки (информации) N³25 их определяют следующим образом.
Среднее значение износа И, мм, определяется по формуле:

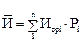 , (46)
, (46)
где Исрi – значение износа в середине i-го интервала;
Рi – опытная вероятность в i-ом интервале.
Для нашего примера:

Среднее квадратическое отклонение определяется по формуле:
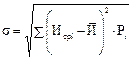 ,мм. (47)
,мм. (47)
Для нашего примера:

= 0,20 мм.
Коэффициент вариации определяется по формуле:
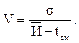 (48)
(48)
Для нашего примера:
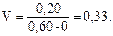
2.3.4 Проверка информации на наличие выпадающих точек
Проверку информации на наличие выпадающих точек осуществляют по формуле:
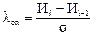 , (49)
, (49)
где Иi и Иi-1 – смежные точки в сводной ведомости информации (см. таблицу 8).
В нашем примере:
для наименьшего значения износа
И1=И2=0,05 мм; И3= 0,20 мм; 
для наибольшего значения износа
И50=1,05 мм; И49=0,95 мм; 
Полученные значения сравнивают с табличными значениями критерия Ирвина (Приложение Б, таблица Б1).
Если λоп < λт то информация достоверна, если же λоп > λт, то такие точки «выпадают», т.е. должны быть исключены из информации как недостоверные. В этом случае необходимо перестроить статистический ряд с учетом уменьшения количества информации за счет выпавших точек и вновь рассчитать основные числовые характеристики.
В нашем случае при N=50 и доверительной вероятности a=0,95 табличное значение критерия Ирвина lТ=1,1 т.е. больше lоп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
Дата добавления: 2015-10-19; просмотров: 2748;
