Вычисление абсолютных, относительных и средних показателей.
|
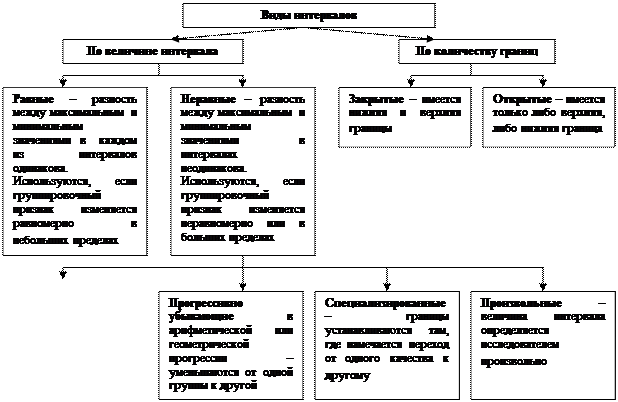
Рис. 7. Виды интервалов статистической группировки
3.4. Ряды распределения: понятие, элементы и виды
Ряд распределения– этогруппировка единиц однородной совокупности по одному признаку, т.е. это простая структурная группировка, в которой для характеристики групп применяется один показатель – численность группы. Он состоит из вариант (хi) и частот (fi). Варианты – это отдельные значения признака. Они могут быть положительными и отрицательными, абсолютными и относительными. Частоты – это числа, показывающие, сколько раз встречаются отдельные значения признака в ряду распределения. Ряд распределения принято оформлять в виде таблицы 5, состоящей из двух колонок (или строк), в одной из которых приводятся варианты в порядке возрастная, а в другой – частоты. Сумма всех частот (∑fi) называется объемом распределения, или его численностью. Достаточно часто в ряд распределения вводятся дополнительные графы, в которых рассчитываются частости и накопленные частоты. Частости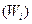 
– это частоты (fi), выраженные в виде относительных величин (доли единиц, процентов), исчисляемые путем деления частоты каждой варианты на общую сумму всех частот: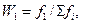 
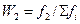и т.д..Сумма частостей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, исчисляются путем последовательного прибавления к частоте первой варианты частот последующих вариант.
Таблица 5
Ряд распределения
| Вариант xi | Частота fi | Частости wi | Накопленные частоты si |
| x1 | f1 | w1= f1 / ∑fi | s1 = f1 |
| x2 | f2 | w2 = f2 / ∑fi | s2 = f1+ f2 |
| +x3 | f3 | w3 = f3 / ∑fi | s3 = f1+ f2+ f3 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| xn | fn | wn = fn / ∑fi | sn = f1+ f2+ f3+…+ fn=∑fi |
| Итого | ∑fi | ∑wi | – |
Виды рядов распределения представлены на рисунке 8.
Рис. 8. Виды рядов распределения
Правила построения ряда распределения аналогичны правилам построения статистической группировки. Наглядно ряды распределения можно представить при помощи их графического изображения. Для этой цели строят графики – полигон, гистограмму, огиву и кумуляту распределения.
Ряд распределения характеризует состав (структуру) и однородность совокупности по изучаемому признаку, закономерность распределения и границы вариации изучаемого признака в совокупности. Различные обобщающие показатели (относительная величина структуры, средние, мода, медиана, дисперсия и т.д.) исчисляются на основе ряда распределения.
Дата добавления: 2015-11-06; просмотров: 995;