Способы выражения и виды
Относительный показатель– это обобщающий показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними. Поэтому по отношению к абсолютным показателям относительные показатели являются вторичными. При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим, или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием, или базой сравнения.
По способу (форме) выраженияотносительные показатели подразделяются на две группы:
1) относительные показатели, полученные в результате соотношения одноименных абсолютных показателей. Результат такого соотношения может быть представлен в форме:
· коэффициента (база сравнения принята за 1);
· процента 0/0 (база сравнения принята за 100);
· промилле 0/00 (база сравнения принята за 1000);
· продецимилле 0/000 (база сравнения принята за 10000);
2) относительные показатели, полученные в результате соотношения разноименных абсолютных показателей. Они, как правило, являются именованными числами. Их наименование представляет собой сочетание наименований сравниваемого и базисного показателей. Например, плотность населения (отношение числа жителей к территории, на которой они живут) определяется количеством человек на 1 км2, количество произведенного мяса на 100 га сельскохозяйственных угодий и т.д.
По своему содержанию относительные показатели подразделяются на виды (типы), представленные в таблице 6.
Относительные показатели позволяют изучать структуру явления, его изменение в пространстве и во времени, взаимосвязи между явлениями, интенсивность изменения или распространения какого-либо явления.
6.4. Средняя величина: понятие, сущность, значение и категории
Средняя величина– это обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу однородной совокупности в конкретных условиях места и времени. Присущие отдельным единицам совокупности значения образуются под действием как общих, так и сугубо индивидуальных и случайных причин, обусловленных особенностями существования и развития каждой единицы совокупности. Последние порождают различия в величине признака у единиц совокупности, называемые вариацией, и отклонения от общего, среднего в ту и другую сторону (т.е. со знаком «+» и «-»). В массовом явлении эти отклонения более или менее взаимно уравновешиваются (погашаются), в результате чего в средней проявляется общее и закономерное, присущее данной совокупности явлений. Это важное свойство средней, делающее метод средних величин действенным средством исследования социально-экономических явлений. Но если средняя вычисляется для совокупности, состоящей из качественно неоднородных единиц, то в ней погашаются и существенные различия? и средняя становится фиктивной, лишенной качественного содержания, не дающей представления о действительности. Поэтому важнейшими условиями правильного исчисления и применения, средних являются качественная
Таблица 6
Виды (типы) относительных показателей
| Наименование показателя | Формула расчета | Пояснение | |
| А | |||
| Группа 1. Относительные показатели, полученные в результате соотношения одноименных абсолютных показателей | |||
| Относительный показатель выполнения плана (ОПВП) | 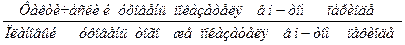
| Выражается в форме коэффициента и процента. Показывает, степень выполнения плана по уровню показателя в i – том периоде | |
| Относительный показатель планового задания (ОППЗ) | 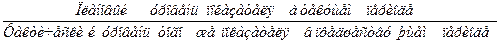
| Выражается в форме коэффициента и процента. Показывает, планируется увеличение или уменьшение уровня показателя в текущем периоде по сравнению с фактическим уровнем этого же показателя за предшествующий период | |
| Относительный показатель динамики (ОПД) | 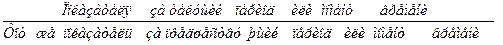 Взаимосвязь показателей:
Взаимосвязь показателей: 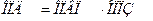
| Выражается в форме коэффициента (коэффициент роста) и процента (темп роста). Характеризует изменения уровня показателя во времени. Показывает, во сколько раз увеличился или уменьшился уровень показателя текущего периода по сравнению с уровнем показателя предшествующего периода | |
| Относительный показатель структуры (ОПС) | 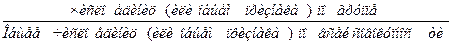
| Выражается в форме коэффициента (доли) и процента (удельного веса). Сумма всех долей равна 1, а удельных весов 100%. Рассчитывается по группированным данным и показывает долю отдельных частей в общем объеме совокупности (структуру совокупности по изучаемому признаку) | |
| Относительный показатель координации (ОПК) | 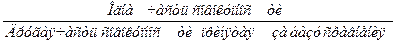
| Характеризует отношение частей данной совокупности к одной из них, принятой за базу сравнения. Показывает, во сколько раз одна часть совокупности больше другой либо сколько единиц одной части приходится на 1, 10, 100, 1000, … единиц другой части | |
| Относительный показатель наглядности (ОПН) | 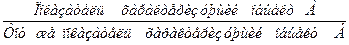
| Выражается в форме коэффициента и процента. Отражает результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду (или моменту) времени, но к разным объектам (предприятиям, районам, областям, странам и т.п.). Показывает, во сколько раз один из сравниваемых показателей больше (или меньше) другого | |
| Группа 2. Относительные показатели, полученные в результате соотношения разноименных абсолютных показателей | |||
| Относительный показатель интенсивности (ОПИ) | 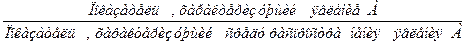
| Характеризует степень распространения изучаемого процесса или явления в определенной среде. Его получают сопоставлением разноименных, но взаимосвязанных в своем развитии показателей. Поэтому часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле. Разновидностью ОПИ являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения | |
однородность совокупности (в отношении признака, по значениям которого она вычисляется) и достаточно большая численность единиц совокупности.
Средние могут вычисляться для совокупности в целом и для отдельных ее групп. Первые называются общими средними (отражают общие черты изучаемого явления), вторые – групповыми или частными средними(отражаютчертыявления, складывающиеся в условиях конкретной группы).
В статистике применяются две категории средних величин:
· степенные средние (к ним относятся средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая, средняя кубическая и др.);
· структурные средние (мода, медиана, квартили, квинтели, децели, перцентели).
Средняя величина всегда именованная, имеет ту же размерность, что и признак у отдельных единиц совокупности. Она применяется для оценки достигнутого уровня изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности хозяйственных единиц, выявления взаимосвязей явлений при прогнозировании, при расчете нормативов.
6.5. Степенные средние: виды и формы
Общая формула расчета степенных средних представлена в таблице 7.
Таблица 7
Общая формула степенной средней
| Форма | Формула расчета | Обозначения |
| А | ||
| Простая (незвешенная) − рассчитывается по несгруппированным данным | 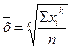
| 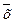 − средняя величина признака; − средняя величина признака;
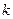 − показатель степени средней; − показатель степени средней;
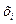 − − 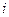 -й вариант (значение) осредняемого признака (i=1, …., n); -й вариант (значение) осредняемого признака (i=1, …., n);
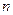 − число вариантов − число вариантов
|
| Взвешенная − рассчитывается по сгруппированным данным | 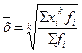
| 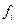 − частота (вес) − частота (вес) 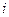 -того варианта, показывающая, сколько раз встречается -того варианта, показывающая, сколько раз встречается 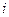 -тое значение осредняемого признака -тое значение осредняемого признака
|
Общая формула расчета степенных средних имеет показатель степени 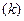 . В зависимости от того, какое значение он принимает, различают виды степенных средних. Их формулы расчета представлены в таблице 8.
. В зависимости от того, какое значение он принимает, различают виды степенных средних. Их формулы расчета представлены в таблице 8.
Таблица 8
Виды степенных средних
| Вид степенной средней | Показатель
степени
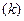
| Формула расчета | Пояснение | |
| простая (незвешенная) | взвешенная | |||
| А | ||||
| Гармоническая | -1 | 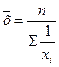
| 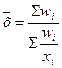
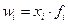
| Взвешенная применяется тогда, когда не известны частоты 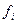 , а известно , а известно 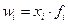 . Простая может использоваться вместо взвешенной в тех случаях, когда значения . Простая может использоваться вместо взвешенной в тех случаях, когда значения 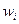 для всех единиц совокупности равны для всех единиц совокупности равны
|
| Геометрическая | 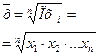
| 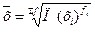
| Простая применяется для расчета среднего коэффициента роста (темпа роста) в рядах динамики, если задана последовательность цепных относительных показателей динамики | |
| Арифметическая | 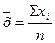
| 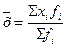
| Простая применяется, когда все частоты равны меду собой. Взвешенная применяется, когда частоты не равны между собой | |
| Квадратическая | 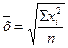
| 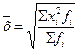
| Наиболее широко этот вид средней применяется при расчете показателей вариации |
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени k увеличивается и соответствующая средняя величина:
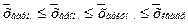
Средняя арифметическая и средняя гармоническая – наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых и при выявлении взаимосвязи между признаками с помощью группировок. Их выбор определяется характером имеющейся в распоряжении исследователя информации.
Определение средней арифметической в ряде случаев требует больших затрат времени. Для упрощения вычисления средних величин используются свойства средней арифметической (без доказательств):
1. Средняя величина от постоянной величины равна ей самой: 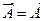 .
.
2. Произведение средней величины на сумму частот равно сумме произведения вариантов на их частоты: 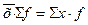 .
.
3. Если каждую варианту увеличить или уменьшить на одну и ту же величину, то средняя величина увеличится или уменьшится на эту же величину: 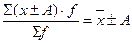 .
.
4. Если каждую варианту увеличить или уменьшить в одно и то же число раз, то средняя величина увеличится или уменьшится в то же число раз: 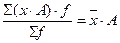 .
.
5. Если все частоты увеличить или уменьшить в одинаковое число раз, средняя величина не изменится: 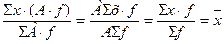 .
.
6. Средняя величина суммы равна сумме средних величин: 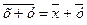 .
.
7. Сумма отклонений всех значений признака от средней величины равна нулю.
Дата добавления: 2015-11-06; просмотров: 1052;
