Лекция 5. Модели потоков событий. Марковский процесс. Одноканальная СМО с ожиданием

Цель лекции: освоение понятий поток событий, простейший поток событий, Марковский процесс.

Содержание

1.Поток событий. Свойства потоков событий. Простейший поток событий. Формула Пуассона.

2. Процесс обслуживания как Марковский процесс.

3. Одноканальная СМО с ожиданием.

Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени.

Примерами могут быть:

- поток вызовов на телефонной станции;

- поток сбоев компьютера;

- поток выстрелов, направляемых на цель, и т.д.

Регулярным потоком называется поток, в котором события следуют одно за другим через одинаковые промежутки времени (детерминированная последовательность событий).

Такой поток событий редко встречается на практике. В телекоммуникационных системах чаще встречаются потоки, для которых и моменты наступления событий и промежутки времени между ними являются случайными.

Рассмотрим такие свойства потоков событий, как стационарность, ординарность и отсутствие последействия.

Поток стационарен,если вероятность появления какого-то числа событий на интервале времени τ зависит только от длины этого интервала и не зависит от его расположения на оси времени. Для стационарного потока среднее число событий в единицу времени постоянно.

Ординарным потоком называется поток, для которого вероятность попадания на данный малый отрезок времени 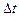двух и более требований пренебрежительно мала по сравнению с вероятностью попадания одного требования.

В системах телекоммуникаций поток принято считать ординарным.

Потокбез последствияхарактеризуется тем, что для двух непересекающихся интервалов времени

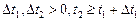
вероятность появления числа событий 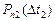на втором интервале не зависит от числа появления событий 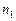на первом интервале.

Параметром потока называется предел

,

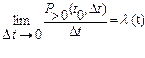где 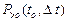— вероятность того, что на интервале 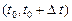появятся заявки.

Интенсивностью потока μ называется среднее число событий в единицу времени.

Для стационарного потока его параметр не зависит от времени .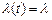

Для стационарного и ординарного потока λ=μ.

Простейшим или пуассоновским потоком называется стационарный, ординарный поток без последействия.

Простейший поток подчиняется пуассоновскому закону распределения

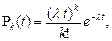
где 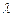— интенсивность потока;

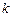— количество событий, появляющихся за время .

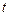Простейший поток можно задать функцией распределения промежутка между соседними вызовами

F(t)=P(z<t)=1-P(z>t),

P(z>t) равносильна вероятности того, что в промежутке длиной t не поступит не одного вызова.

F(t)=P(z>t)=1- 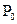(t)=1-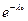

Данный закон распределения случайной величины называется показательным.

Свойства и характеристики простейшего потока:

а) для простейшего потока математическое ожидание и среднеквадратическое отклонение величины промежутка z равны между собой MZ= σz=1/λ;

б) Математическое ожидание и дисперсия числа вызовов i за промежуток времени t равны между собой Mi=Di= λt.

Совпадение этих величин используют на практике при проверке реального потока для соответствия его простейшему.