Теорема Джексона

Рассмотрим сеть, содержащую N узлов, причем каждый i – ый узел состоит из m_i серверов с показательным распределением времени обслуживания с параметром μ_i . В каждый узел поступает простейший поток заявок с интенсивностью γ_i . Покидая i – ый узел, заявка с вероятностью r_ij поступает в j – ый узел. Вероятность того, что заявка после обслуживания в i – ом узле вообще покинет сеть, будет равна 1 - ∑ r_{ij .}

Полная интенсивность потока λ_i , поступающего в i – ый узел, будет равна

λ_i = γ_i + ∑ λ_j r_ij , где i = 1,2,3, … , N.

Состояние сети с N узлами описывается вектором, компонентами которого являются количества заявок в каждом из узлов сети (k₁, k₂, … , k_N).

Джексону удалось доказать, что стационарная вероятность этого состояния раскладывается в произведение безусловных распределений

p(k₁, k₂, … , k_N) = p₁(k₁), p₂(k₂), … , p_N(k_N),

которые представляют собой стационарные вероятности для системы M/M/m. Этот результат носит название теорема Джексона.

Другими словами каждый узел в сети ведет себя так, как если он был независимой СМО типа M/M/m.

Лекция 8. Основные понятия теории планирования экспериментов

Цель лекции: изучение основ теории планирования экспериментов.

Содержание

1. Необходимость планирования экспериментов.

2. Стратегическое планирование эксперимента.

3. Тактическое планирование эксперимента

Теория исходит из абстрактной схемы сложной системы, называемой «чер­ным ящиком» (рисунок 8.1). Считается, что исследователь может наблюдать вхо­ды и выходы «черного ящика» (имитационной модели) и по результатам на­блюдений определять зависимость между входами и выходами.

Эксперимент на имитационной модели будем рассматривать состоящим из наблюдений, а каждое наблюдение — из прогонов модели.

Входные переменные х₁, х₂, ..., х_т называются факторами. Выходная пере­менная у называется наблюдаемой переменной (реакцией, откликом).

Факторное пространство — это множество факторов, значения которых ис­следователь может контролировать в ходе подготовки и проведения модель­ного эксперимента.

Рисунок 8. 1 - Абстрактная схема системы

Каждый фактор имеет уровни. Уровни — это значения, которые устанавли­ваются для каждого фактора при определении условий прогона модели в на­блюдении.

Целью эксперимента является нахождение функции у, при этом предпола­гается, что значение отклика складывается из двух составляющих:

y = f(x_l,x₂, ..., х_m,) + е(х₁х₂, ..., х_т),

где f(x_l,x₂, ..., х_т) -функция отклика (неслучайная функция факторов);

е(х₁х₂, ..., х_т ) - ошибка эксперимента (случайная величина);

х₁х₂, ..., х_т - определенное сочетание уровней факторов из факторного пространства.

Очевидно, что у является случайной переменной, так как зависит от случай­ной величины е(х₁х₂, ..., х_т). Дисперсия D [у], которая характеризует точность измерений, равна дисперсии ошибки опыта: D [у] = D [е].

Дисперсионный анализ — это статистический метод анализа результатов на­блюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния.

В условиях эксперимента факторы могут варьировать, благодаря чему можно иссле­довать влияние фактора на наблюдаемую переменную. Если влияние неко­торого фактора на наблюдаемую переменную изменяется при изменении уровня некоторого другого фактора, говорят, что между факторами существует взаимодействие.

Эксперимент, в котором реализуются все возможные сочетания уровней фак­торов, называется полным факторным экспериментом (ПФЭ).

Общее число различных сочетаний уровней в ПФЭ для т факторов можно вычислить по формуле:

S = k₁ · k₂ · k₃ · ... k_i · ... · k_m,

где к_i — число уровней i-го фактора.

Если число уровней для всех факторов одинаково, то S = k^m. Каждому соче­танию уровней факторов соответствует одно наблюдение.

Недостаток ПФЭ — большие затраты на подготовку и проведение, так как с увеличением числа факторов и их уровней число наблюдений в эксперименте растет. Например, если имеется шесть факторов с двумя уровнями каждый, то даже при одном прогоне модели в каждом наблюдении нужно S = 2⁶ = 64 на­блюдения. Очевидно, что каждый прогон удваивает это число, следовательно, увеличивает затраты машинного времени.

Такого рода задачи и явились одной из причин возникновения теории пла­нирования экспериментов.

Планирование экспериментов — один из разделов математической статистики, изучающий рациональную организацию измерений, подверженных случай­ным ошибкам.

Планом эксперимента называется совокупность значений факторов, при ко­торых находятся значения оценок функции отклика, удовлетворяющих не­которому критерию оптимальности, например, точности.

Различают стратегическое планирование эксперимента и тактическое пла­нирование эксперимента.

Стратегическое планирование эксперимента

Целью стратегического планирования эксперимента является определение ко­личества наблюдений и сочетаний уровней факторов в них для получения на­иболее полной и достоверной информации о поведении системы.

При стратегическом планировании эксперимента должны быть решены две основные задачи.

1. Идентификация факторов.

2. Выбор уровней факторов.

Под идентификацией факторов понимается их ранжирование по степени вли­яния на значение наблюдаемой переменной.

По итогам идентификации целесообразно разделить все факторы на две груп­пы — первичные и вторичные.

Первичные — это факторы, исследование которых необходимо провести.

Вторичные — факторы, которые не являются предметом исследования, но влиянием которых нельзя пренебречь.

Выбор уровней факторов производится с учетом двух противоречивых требо­ваний:

- уровни фактора должны перекрывать весь возможный диапазон его измене­ния;

- общее количество уровней по всем факторам не должно приводить к боль­шому количеству наблюдений.

Отыскание компромиссного решения, удовлетворяющего этим требованиям, и является задачей стратегического планирования эксперимента.

Так как ПФЭ может потребовать много машинного времени, необходимо располагать методами отбора факторов, оказывающих существенное влияние на отклик. Если исследователя не интересуют взаимодейст­вия высокого порядка, можно получить большое количество информации с помощью исследования лишь некоторой части (1/2,1/4, 1/8 и т. д.) всех воз­можных сочетаний уровней факторов.

Если в эксперименте производится лишь часть возможных наблюдений, т. е. уменьшается выборка, эксперимент называется частичным факторным экспе­риментом (ЧФЭ).

Когда используется выборка меньшая, чем того требует ПФЭ, плата за это осуществляется риском смешивания эффектов. Под смешиванием понимает­ся то, что исследователь, измеряя один эффект, в то же время измеряет, воз­можно, и некоторый другой эффект. Например, если главный эффект сме­шивается с взаимодействием более высокого порядка, то эти два эффекта уже невозможно отделить друг от друга.

При построении плана ЧФЭ исследователь должен определить эффекты, сме­шивание которых он может допустить. Успех ЧФЭ достигается в случае, если его план позволяет не смешивать ни один главный эффект с другим.

Если число факторов невелико (обычно меньше пяти), то ЧФЭ нецелесооб­разен вследствие смешивания эффектов, не позволяющего различить главные эффекты и важные взаимодействия.

В качестве примера рассмотрим план дробного факторного эксперимента (ДФЭ) — одного из видов ЧФЭ, с полным числом возможных сочетаний 2⁵. В ДФЭ каждый фактор имеет два уровня — нижний и верхний, поэтому общее число наблюдений S = 2^т.

Тактическое планирование эксперимента

Целью тактического планирования эксперимента является определение необ­ходимого количества прогонов модели в каждом наблюдении.

Так как имитационное моделирование представляет собой статистический эксперимент, то при его проведении необходимо получить достоверный ре­зультат с заданной точностью.

В общем случае количество прогонов модели (объем выборки), необходимое для получения оценок наблюдаемой переменной с заданной точностью, за­висит от следующих факторов:

- вида распределения наблюдаемой переменной;

- коррелированности между собой элементов выборки.

При отсутствии сведений о перечисленных факторах для повышения точности оценок истинного значения наблюдаемой переменной увеличивается количество прогонов модели (объем выборки) для каждого наблюдения, т. е. для каждого сочетания уровней факторов, выбранного на этапе стратегического плани­рования эксперимента.

Если случайные значения наблюдаемой переменной не коррелированны и их распределение не меняется от прогона к прогону, то выборочное среднее можно считать нормально распределенным. Для случая, когда целью модели­рования является определение среднего значения некоторого случайного пара­метра, требуемое число прогонов N_T модели в каждом наблюдении опреде­ляется по формуле

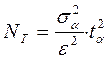(8.1)

где ε — точность оценки;

s_α — среднеквадратическое отклонение;

t_α — аргумент функции Лапласа, при заданном уровне значимости α/2 на­ходится по таблице 1, в которой даны наиболее актуальные пары α и t_α.

Т а б л и ц а 8.1

Список литературы.

1. Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высшая школа, 1998.

2. Ермаков С.М., Михайлов Г.А. Курс статистического моделирования. – М.: Радио и связь, 1976.

3. Крылов В.В., Самохвалова С.С. Теория телетрафика и её приложения. - СПб.: БХВ - Петербург, 2005.

4. Шварц М. Сети связи: Протоколы, моделирование и анализ. - М.: Наука, 1992.

5. Боев В.Д. Моделирование систем. Инструментальные средства GPSS World: Учеб. пособие. – СПб.: БХВ-Петербург, 2004.

6. Кудрявцев Е.М. GPSS World. Основы имитационного моделирования различных систем. – М.: ДМК Пресс, 2004.

7. Томашевский В., Жданова Е. Имитационное моделирование в среде GPSS. - М.: Бестселлер, 2003.

8. Учебное пособие по GPSS World. – Казань: Изд-во «Мастер Лайн», 2002.

9. Руководство Пользователя по GPSS World. – Казань: Изд-во «Мастер Лайн», 2002.

Содержание

Введение …………………………………………………………………………..3

Лекция 1…………………………………………………………………………....4

Лекция 2……………………………………………………………………………8

Лекция 3…………………………………………………………………………..12

Лекция 4…………………………………………………………………………..16

Лекция 5…………………………………………………………………………..20

Лекция 6…………………………………………………………………………..24

Лекция 7…………………………………………………………………………..28

Лекция 8…………………………………………………………………………..32

Список литературы ……………………………………………………………...36