Лекция 6. Уравнения Колмогорова. Схема гибели и размножения

Цель лекции: изучить правило составления уравнений Колмогорова.

Освоить методы нахождения предельных вероятностей для установившихся режимов.

Содержание

1. Общее правило составления уравнений Колмогорова.

2. Схема гибели и размножения.

3. Формула Литтла.

4. Одноканальная СМО с отказами.

Познакомимся с общим правилом составления уравнений Колмогорова. Рассмотрим граф переходов из предыдущей лекции.

В левой части уравнения стоит производная вероятности -го состояния; в правой части — сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного ( -го) состояния.

Построим по этому правилу систему дифференциальных уравнений

,

,

. . .

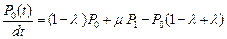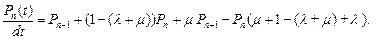
После преобразований получаем

,

,

. . .

.

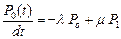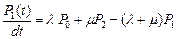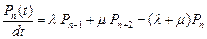Эти уравнения могут быть решены при начальных условиях

,

,

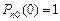частотными методами с использованием преобразования Лапласа.

Чаще интересуются установившимся или стационарным режимом, для которого справедливо

.

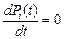В этом случае система дифференциальных уравнений преобразуется в систему линейных уравнений:

,

,

. . .

,

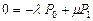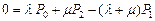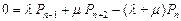отсюда , , .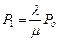

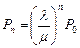Учитывая, что 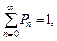получаем

,

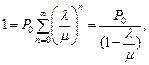
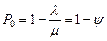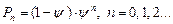
Параметр выражает степень насыщения в системе и называется загрузкой или коэффициентом использования СМО. Для одноканальных СМО при 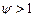установившегося режима не существует, очередь растет неограниченно.

Установившийся режим не зависит от начальных условий. Получим некоторые числовые характеристики установившегося режима.