Лекция 7. Сети СМО
Цель лекции: изучить методы анализа сетей СМО.
Содержание
1. Определение сети СМО. Замкнутые и разомкнутые сети.
2. Граф и матрица передач.
3. Характеристики сети СМО.
4. Теорема Джексона.
В общем случае сеть СМО (Queuing Networks) можно представить в виде графа, вершинами которого являются одноканальные и многоканальные СМО (дуги определяют потоки передачи требований).
Простейшая разомкнутая или открытая сеть получается при последовательном соединении СМО (рис.7.1). Она еще называется многофазной СМО.
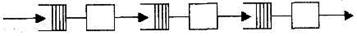
Рисунок 7.1
Различают замкнутые и разомкнутые сети. Для замкнутой вероятностной сети не существует внешних источников требований, то есть в ней всегда находится одно и то же количество требований. Для разомкнутой сети имеются источники требований и стоки требований.
Для расчетов сетей массового обслуживания используется теория вероятностных сетей, которая основывается на марковских и полумарковских процессах, но большинство результатов получено только для экспоненциальных законов распределения. При количестве узлов сети больше трех для расчетов используются численные приближенные методы. Операционный анализ в отличие от теории массового обслуживания опирается на логику работы рассматриваемой или моделируемой системы. Это позволяет установить простые зависимости между параметрами и показателями работы системы, не абстрагируясь от процессов ее функционирования.
Основная задача операционного анализа вероятностных сетей состоит в определении таких показателей, как среднее время пребывания требований в отдельных узлах сети, загрузка устройств в узлах, средние длины очередей к узлам и т.п.
Большинство результатов операционного анализа касается замкнутых сетей, когда требования, которые покидают сеть, снова возвращаются в нее. Замкнутые сети можно использовать, когда рассматриваемая система работает с перегрузкой. В этом случае можно считать, что вместо требования, которое покинуло систему, в систему поступает другое требование с такими же параметрами.
Сеть СМО удобно представлять в виде графа передач (рисунок 7.2), где вершины графа соответствуют СМО, дуги указывают возможности перехода заявки из одной СМО в другую, а числа в дугах — вероятности перехода.

Рассмотрим сеть систем массового обслуживания, которая включает M СМО и один источник заявок. Заявки, выходящие из 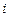 -й системы
-й системы  с постоянной вероятностью
с постоянной вероятностью  , поступают в систему
, поступают в систему 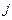 или покидают сеть
или покидают сеть 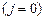 . Из источника в
. Из источника в 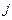 -ю систему заявки поступают с вероятностью
-ю систему заявки поступают с вероятностью 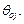 Матрицу вероятностей поступления требований из одной системы в другую называют матрицей передач:
Матрицу вероятностей поступления требований из одной системы в другую называют матрицей передач:

где 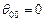 — циркулирование потока заявок в источнике,
— циркулирование потока заявок в источнике,
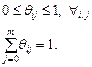
Для графа передач, представленного на рис.5.2, матрица передач будет следующей
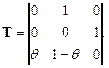
Для определения характеристик сети СМО необходимо определить интенсивности потоков заявок в каждой системе, т.е. среднее число заявок, поступающих в систему за единицу времени в установившемся режиме 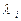 . Среднее число заявок, покидающих систему, равно среднему числу поступающих заявок, и, следовательно,
. Среднее число заявок, покидающих систему, равно среднему числу поступающих заявок, и, следовательно,
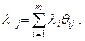
В матричной форме это выражение имеет вид:
.
Интенсивности потоков заявок в СМО зависят от 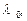 следовательно, можно определить:
следовательно, можно определить:
 ,
,
где 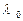 — интенсивность источника заявок (интенсивность потока, поступающего на вход сети).
— интенсивность источника заявок (интенсивность потока, поступающего на вход сети).
Допустим, сеть замкнута, и в ней циркулирует конечное число заявок.
Тогда

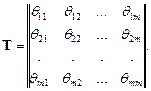
Здесь интенсивности потоков определяются общим числом требований в сети. Выбрав некоторую СМО 
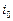 за базовую, можно определить
за базовую, можно определить
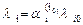 .
.
Важной характеристикой сети СМО служит среднее время пребывания в ней заявки. Пусть сеть разомкнута. В установившемся режиме вероятность нахождения заявки в СМО определяется
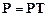
Сравнивая с  ,получаем:
,получаем:
 ,
,
где 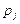 — вероятность нахождения заявки в
— вероятность нахождения заявки в 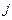 -й СМО.
-й СМО.
Относительная частота прохождения требования через систему j за достаточно большой интервал времени t:
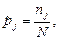

где 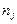 — число случаев, когда заявка оказалась в системе
— число случаев, когда заявка оказалась в системе 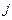 ;
;
 — общее число заявок, прошедших через сеть.
— общее число заявок, прошедших через сеть.
Тогда
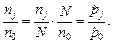
При достаточно большом интервале времени
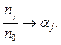
Таким образом, требования, поступающие из источника, 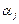 раз проходят через систему с номером
раз проходят через систему с номером 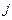 ,прежде чем вернуться в источник.
,прежде чем вернуться в источник.
Следовательно,
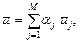
где 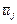 — среднее время пребывания заявки в СМО с номером
— среднее время пребывания заявки в СМО с номером 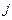 .
.
Сложность расчета сетей СМО заключается в том, что простейший поток заявок, поступающий в систему, на ее выходе в общем случае будет обладать последействием. А в этом случае нельзя применять рассмотренный выше аппарат анализа марковских СМО. Однако, если на всех приборах сети длительность обслуживания распределена по показательному закону, то выходящие из СМО потоки заявок будут пуассоновскими. Такие сети называются показательными.
Для показательных сетей существует установившийся режим, если для каждой 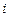 -й СМО загрузка
-й СМО загрузка 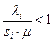 .
.
Дата добавления: 2015-10-05; просмотров: 3617;
