Процесс обслуживания как марковский случайный процесс

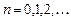Пусть система может находиться в состояниях где — в системе находится 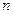заявок. Обозначим вероятность нахождения системы в конкретном состоянии 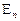в момент времени 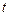через 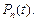Очевидно, что для каждого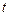

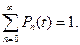
Если переход из состояния 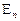в зависит только от этих состояний и не зависит от предыдущих 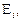то такая последовательность во времени будет марковским процессом. Таким образом, система с ожиданием в случае простейшего потока и показательного времени обслуживания представляет собой случайный процесс Маркова.

Каждой паре состояний 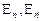можно поставить в соответствие условную вероятность 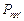того, что система находится в состоянии 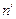в момент 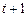при условии, что в момент 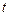она находилась в состоянии .

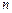Очевидно, что для вероятности 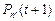можно написать

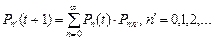(5.1)

Это уравнение означает, что система может оказаться в состоянии 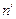путем одного из многих 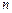несовместных переходов. Причем вероятность нахождения системы в состоянии 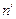при условии, что ранее система находилась в состоянии n, по формуле произведения вероятностей событий равна 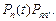Если 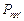равна нулю, то переход из состояния 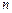в 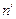невозможен.

Соотношение (5.1) может быть записано в векторной форме

(5.2)

где квадратная матрица 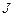образована из элементов 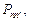удовлетворяющих условиям

,

.

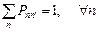Из условия ординарности входного потока следует, что в каждый момент времени может прийти не более одной заявки и покинуть систему не более одной заявки. Отсюда

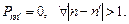
Матрица, удовлетворяющая этим условиям, называется матрицей переходов, вероятности 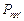— вероятности перехода. Из (5.2) следует, что для однородной последовательности Маркова, определяемой как последовательность, для которой значения элементов матрицы 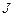постоянны (не зависят от номеров состояний), имеем:

,

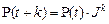в частности,

,

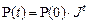т.е. марковская последовательность целиком определяется матрицей перехода 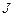и начальными условиями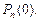

Пусть имеется одноканальная система с простейшим потоком на входе с интенсивностью 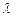и экспоненциальным временем обслуживания с показателем . 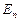— состояние системы, когда в ней находится n заявок. За момент времени 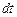может прийти одна заявка с вероятностью , ноль заявок с вероятностью 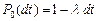, может быть обслужена одна заявка с вероятностью 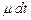и не обслужена ни одна заявка с вероятностью 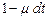. Матрица переходов 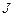будет выглядеть следующим образом

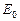
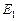
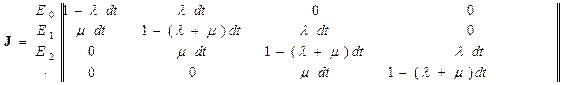
Вероятность 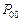определяется вероятностью отсутствия прихода заявок за время 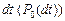. Вероятность 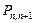определяется вероятностью прихода одной заявки 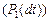, а вероятность 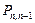определяется вероятностью обслуживания одной заявки. Вероятность 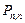определяется вероятностью составного события: заявка не придет и не будет обслужена.

Более компактно матрицу перехода можно представить в виде графа переходов, в котором вершины означают состояния системы, а дуги — вероятности переходов.

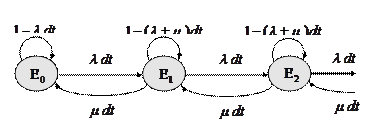Рисунок 5.1