Центральные моменты СВ. Дисперсия

Пусть 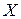– СВ с математическим ожиданием 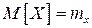. Рассмотрим отклонение СВ 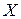от ее математического ожидания: .

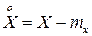Отклонение СВ 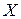от ее математического ожидания называется центрированной случайной величиной .

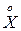Математическое ожидание центрированной СВ равно 0: .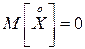

Центральным моментом k-го порядка 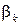случайной величины 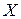называется математическое ожидание от k-той степени соответствующей центрированной случайной величины:

.

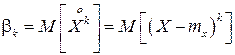Для дискретной СВ: .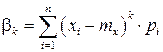

Для непрерывной СВ: .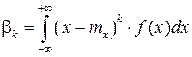

Центральный момент 1-го порядка 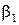есть математическое ожидание и равен 0.