Стандартных распределений ДСВ
| Закон распределения | Математическое ожидание 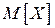
| Дисперсия 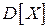
|
| Биномиальный | 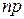
| 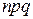
|
| Закон Пуассона | 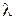
| 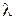
|
| Геометрический | 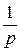
| 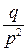
|
| Гипергеометрический | 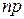
| 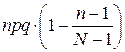
|
Пример.Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10? Найти математическое ожидание и дисперсию случайной величины Х – числа попаданий в цель.
Решение.Вероятность 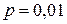 очень мала, а число выстрелов (опытов) достаточно велико. Поэтому искомую вероятность будем находить, используя формулу Пуассона. Случайная величина Х – число попаданий в цель. Требуется найти
очень мала, а число выстрелов (опытов) достаточно велико. Поэтому искомую вероятность будем находить, используя формулу Пуассона. Случайная величина Х – число попаданий в цель. Требуется найти 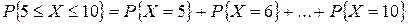 . Имеем:
. Имеем: 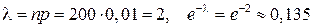 ,
,
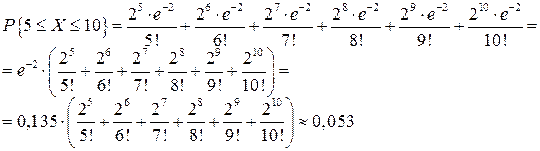
Искомая вероятность приближенно равна 0,053, а числовые характеристики данной случайной величины 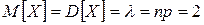 .
.
Пример. Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Найти математическое ожидание и дисперсию случайной величины 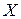 – числа выстрелов по цели до первого попадания.
– числа выстрелов по цели до первого попадания.
Решение.Случайная величина 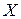 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 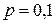 . Тогда
. Тогда 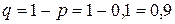 .
.
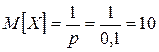 ,
, 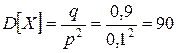 .
.
Дата добавления: 2015-10-19; просмотров: 844;
