Аппроксимация на основе типовых распределений.
Задача аппроксимации на основе типовых распределений решается итерационно и включает выполнение трех основных шагов:
предварительного выбора вида закона распределения;
определения оценок параметров закона распределения;
оценки согласованности закона распределения и ЭД.
Если заданный уровень согласованности достигнут, то задача считается решенной, а если нет, то шаги повторяются снова, начиная с первого шага, на котором выбирается другой вид закона, или начиная со второго – путем некоторого уточнения параметров распределения.
Выбор вида закона распределения осуществляется посредством анализа гистограммы распределения, на предмет их «похожести» типовым распределениям и оценок степени похожести. По степени "похожести" гистограммы типовых законов или по "близости" значений оценок коэффициентов и диапазонов их теоретических значений выбираются распределения – кандидаты для последующей оценки параметров. На рис. 1- 3 представлены графики типовых функций плотностей распределения, часто применяемых в задачах аппроксимации ЭД,
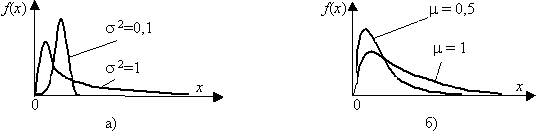
Рис.1. Логарифмически нормальное распределение.
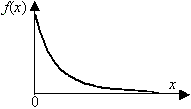
Рис.2. Экспоненциальное распределение.
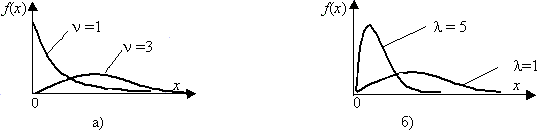
Рис.3. Гамма-распределение.
После выбора подходящего вида распределения производится оценка его параметров, используя математические методы (максимального правдоподобия, моментов или квантилей). В целях упрощения решения задачи в табл.1 приведены расчетные формулы для вычисления оценок параметров типовых распределений.
Таблица 1
| Тип распределения | Оценка параметров распределения по выборочным данным |
| Нормальное | 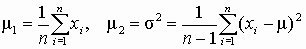
|
| Логарифмически нормальное | 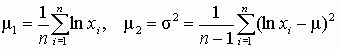
|
| Экспоненциальное | 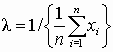
|
| Гамма-распределение | 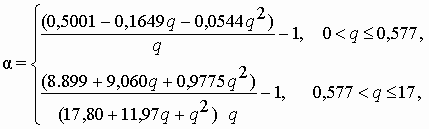 где q=ln( 1/6), где q=ln( 1/6), 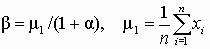
|
Применительно к выбранному закону распределения производится проверка гипотезы о том, что имеющаяся выборка может принадлежать этому закону. Если гипотеза не отвергается, то можно считать, что задача аппроксимации решена. Если гипотеза отвергается, то возможны следующие действия: изменения значений оценок параметров распределения; выбор другого вида закона распределения; продолжение наблюдений и пополнение выборки. Конечно, такой подход не гарантирует нахождение "истинного" или даже подбора подходящего закона распределения.
Дата добавления: 2015-11-12; просмотров: 1770;
