Сущность метода наименьших квадратов.

Метод наименьших квадратов (МНК) - метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.

Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:

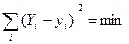
где Y – теоретическое значение измеряемой величины,

y – экспериментальное.

При этом полученные с помощью МНК параметры модели являются наиболее вероятными.

Пример. На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда

y = kx

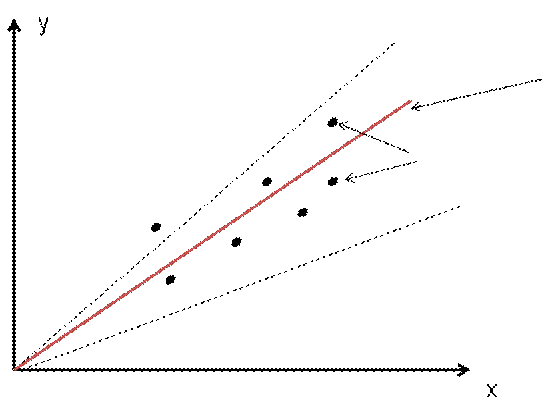
Рис. 4. Сущность МНК.

Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением n = a + b/λ², то на графике строят зависимость n от λ^-2.

Рассмотрим зависимость y = kx(прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой

.

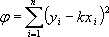Величина φ всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум

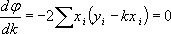
или
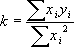(19)

Вычисление показывает, что среднеквадратичная ошибка определения величины k равна при этом

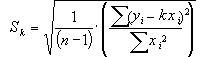, (20)
где – n число измерений.