Показательное распределение

Говорят, что случайная величина 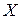имеет показательное распределение с параметром 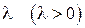, если ее плотность распределения имеет вид: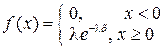

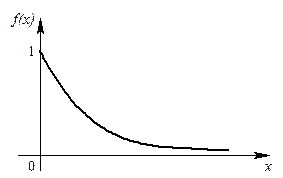
Рис. 7. Кривая показательного распределения

Функция распределения имеет вид:

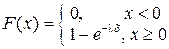
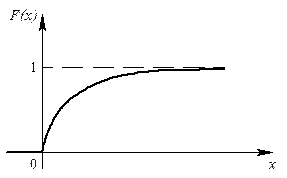
Рис. 8. График функции показательного распределения

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «не старения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

В большинстве случаев время безотказной работы элемента, например электрической лампочки, распределено по показательному закону.

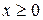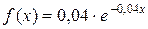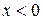Пример.Непрерывная случайная величина Х распределена по показательному закону, заданному при плотностью распределения ; при функция 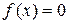. Найти вероятность того, что в результате испытания Х попадет в интервал .

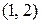Решение.Используем формулу .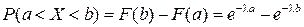

Учитывая, что по условию 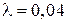, , 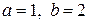получим:

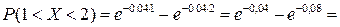0,961– 0,923=0,038.