Правило трех сигм

Сформулируем теперь «правило трёх сигм»: практически достоверно, что если случайная величина распределена нормально, абсолютное отклонение ее от математического ожидания не превосходит утроенного среднеквадратического отклонения:

.

Или – вероятность того, что случайная величина отклониться от своего математического ожидания на величину, большую утроенного среднеквадратического отклонения, равна:

.

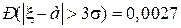Смысла в запоминании числа 0,0027 нет никакого, а вот помнить, что почти вся масса нормального распределения сосредоточена в границах 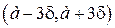, всегда полезно.