Нормальное распределение

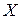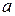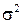Говорят, что случайная величина имеет нормальное распределение с параметрами и , где 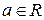, , 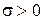если 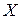имеет следующую плотность распределения: .

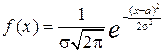Параметр 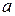есть математическое ожидание нормально распределенной случайной величины, 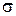– среднеквадратическое отклонение.

Кривая нормального распределения имеет вид (рис. 9):

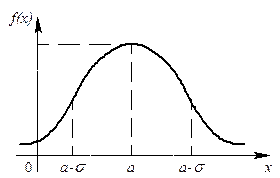
Рис. 9. Кривая нормального распределения с параметрам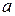и и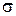

Нормальное (иначе называемое гауссовским по имени Карла Гаусса) распределение играет исключительно важную роль в теории вероятностей, поэтому мы очень подробно изучим все свойства этого распределения.