Для независимых событий

Событие В называют независимым от события А, если появление события А не изменяет вероятности появления события В, то есть условная вероятность события В равна его безусловной вероятности, то есть Р(В|А)=Р(В).

Если событие В не зависит от события А, то и событие А не зависит от события В, то есть свойство независимости событий взаимно.

Для независимых событий теорема умножения (формула 1.23) имеет вид

Р(АВ) = Р(А) ∙Р(В) (1.26)

то есть, вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Для n независимых событий P(A₁, A₂, …, A_n) = 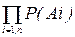(1.27)

Если P(A_i) = p = const, то P(A₁, A₂, …, A_n) = pⁿ. (1.28)

На практике заключение о независимости событий делают по смыслу задачи.

Пример 1.53.Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием равна 0,8, а вторым – 0,7..

Решение. Пусть событие А={поражение цели первым орудием}, событие В={поражение цели вторым}. Вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события А и В независимые. Поэтому по теореме умножения (формула 1.26) искомая вероятность равна

Р(АВ) = Р(А)∙Р(В) = 0,7∙0,8 = 0,56.

Пример 1.54. Рассмотрим пример 1.49 (раздел 1.10.4) с урной, содержащей N шаров, из которых n белых, но изменим опыт: вынув шар, мы кладем его обратно и только затем вынимаем следующий (выборка с возвращением). Какова вероятность того, что оба вынутых шара белые?

Решение. Пусть событие А={первым вынули белый шар}, событие В={первым вынули черный шар}, а С= {вторым вынули белый шар}. Тогда

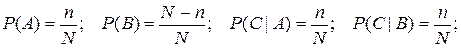
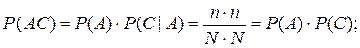
то есть, согласно формуле (1.26) в данном случае события А и С независимы.

Таким образом, при выборке с возвращением результаты второго опыта не зависимы от результатов первого опыта, а при выборке без возвращения они были зависимы. Однако при больших N и n эти вероятности очень близки друг к другу. Этим пользуются, так как иногда производят выборку без возвращения (например, при контроле качестве, когда тестирование объекта приводит к его разрушению), а расчеты проводят по формулам для выборки с возвращением, которые проще.

На практике при расчете вероятностей часто пользуются правилом, согласно которому из физической независимости событий следует их независимость в теоретико-вероятностном смысле.

Пример 1.55. Вероятность того, что человек в возрасте 60 лет не умрет в ближайший год, равна 0,91. Страховая компания страхует на год жизнь двух людей 60-ти лет. Оценить вероятности возможных страховых случаев.

Решение.

Пусть событие А={ первый не умрет}, событие В= {второй не умрет}. Рассмотрим различные сочетания этих событий:

а) вероятность того, что ни один не умрет, равна

P(AB)=Р(А) ∙Р(В)=0,91∙0,91 = 0,8281.

б) вероятность того, что они оба умрут, равна

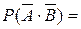(1 – Р(А)) ∙(1 – Р(В)) = (1 – 0,91)∙(1 – 0,91) = 0,0081.

в) вероятность того, что умрет хотя бы один, равна

(1 ‑ Р(АВ)) = 1 – Р(А) ∙Р(В) = 1 – 0,91∙0,91 = 0,1719.

г) вероятность того, что умрет один, равна:

Р(А) ∙(1- Р(В)) +(1- Р(А)) ∙Р(В) = 0,91∙(1–0,91)+ (1 – 0,91)∙0,91 = 0,1638

Система событий А₁, А₂, …, А_n называется независимой в совокупности, если вероятность произведения этих событий равна произведению вероятностей для любой комбинации сомножителей этой системы, то есть

Р(А₁∙А₂∙ … ∙А_n) = Р(А₁)∙Р(А₂) ∙ … ∙Р(А_n). (1.29)

Пример 1.56. Шифр сейфа состоит из 7-ми цифр. Чему равна вероятность того, что вор с первого раза наберет его верно?

Решение. Чтобы с первого раза верно набрать все семь цифр, должны состояться все события, состоящие в том, что вор правильно наберет каждую из цифр, то есть эти события являются совместными. Следовательно Р(А) = Р(А₁∙А₂∙ … ∙А₇)

Так как события А_i независимые и вероятность каждого события равна Р(А_i) = р=1/10, согласно правилу (1.16) имеем Р(А) = Р(А₁)∙Р(А₂)∙…∙Р(А₇) = (1/10)⁷.

Пример 1.57. В более общем виде задача о страховке: вероятность того, что человек в возрасте 60 лет не умрет в ближайший год, равна р=0,91. Страховая компания страхует на год жизнь n людей этого возраста.

а) вероятность того, что ни один из них не умрет согласно формуле (1.28) равна: рⁿ (не придется платить страховую премию никому)-события независимы, совместны.

б) вероятность того, что они все умрут, равна: (1 – 0,91)ⁿ (самые большие выплаты).

в) вероятность того, что умрет один, равна: n∙(1– р)∙р^n-1 (если их перенумеровать, то умерший может иметь номер 1, 2, …, n – это n разных событий, каждое из которых имеет вероятность (1-р)∙р^n-1).

Домашнее задание: ДР-1.8