Вероятность суммы двух совместных событий

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.

Суммой А+В двух совместных событий А и В называют событие С, состоящее в появлении события А, или события В, или обоих этих событий.

Например, если из орудия произведены два выстрела и А- попадание при первом выстреле, В - попадание при втором выстреле, то А+В - попадание при первом выстреле или при втором , или при обоих выстрелах.

Пример 1.46.А – {появление четырех очков при бросании игрального кубика}; В – {появление четного числа очков}. Событии А и В совместные.

Пусть события А и В совместные, причем вероятности этих событий известны. Для таких событий справедлива следующая теорема сложения.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р(А+В) = Р(А) + Р(В) – Р(АВ) (1.21)

Доказательство. Поскольку события А и В совместны, то событие А+В (хотя бы одно) наступит, если наступит одно из следующих трех событий: 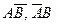или АВ. Эти события несовместны. По теореме сложения двух несовместных событий

(*)

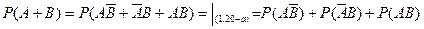Событие А произойдет, если наступит одно из двух несовместных событий: 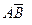или АВ. По теореме сложения двух несовместных событий имеем

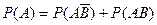
Отсюда (**)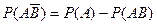

Аналогично имеем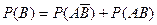

Отсюда (***)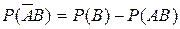

Подставив (**) и (***) в (*), окончательно получим

Р(А+В) = 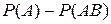+ + 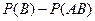Р(АВ)= P(А) + P(В) – P(АВ)

То есть, Р(А+В) = P(А) + P(В) – P(АВ) что и требовалось доказать

Пример 1.47. Вероятности попадания в цель при стрельбе первого и второго орудий , соответственно, равны: р₁=0,7; р₂ = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. Вероятность попадания в цель хотя бы одним из орудий можно рассмотреть состоящим из событий: А – попадание первым орудием; В – попадание вторым орудием; АВ – попадание обоими орудиями. Согласно теореме

Р(А+В) = Р(А) + Р(В) – Р(АВ)

Так как эти события независимы, то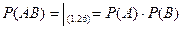

Получим Р(А+В) = Р(А) + Р(В) – Р(А) ∙Р(В)= 0,7+0,8-0,7∙0,8 = 0,94.

Пример 1.48. Из 20 студентов 5 человек сдали на двойку экзамен по истории, 4 по английскому языку, причем 3 студента получили двойки по обоим предметам. Каков процент студентов в группе, не имеющих двоек по этим предметам?

Решение. Решим задачу, используя противоположное событие 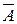- процент студентов, имеющих двойки по этим предметам. Вероятность события 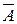равна q= 5/20 + 4/20 – 3/20. искомая вероятность равна р = 1- q = 1 – (5/20 + 4/20 – 3/20) = 0,7 (70%).