Условная вероятность

Событие называется случайным (стохастическим), если при осуществлении совокупности условий S это событие может произойти или не произойти.

Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такая вероятность называется безусловной. Если же налагаются и другие дополнительные условия, то вероятность события называется условной.

Например, требуется определить вероятность случайного события В при условии, что произошло случайное событие А, имеющее ненулевую вероятность. То, что событие А произошло, сужает пространство элементарных событий до множества А, соответствующего этому событию. Дальнейшие рассуждения проведем на примере классической схемы.

Пусть полная группа событий Ω состоит из n равновозможных элементарных событий (исходов) и событию А благоприятствует m(A), а событию АВ благоприятствует m(AB) исходов. Обозначим условную вероятность события В при условии, что А произошло, – Р(В| А). По определению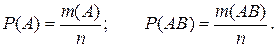

Если А произошло, то реализован один из m(А) исходов, и событие В может произойти , только если произойдет один из исходов, благоприятствующих АВ; таких исходов m(AB). Поэтому естественно положить условную вероятность события В при условии, что А произошло, равной отношению

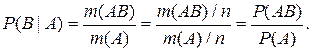
Таким образом, условной вероятностью Р_А(В) или Р(В|А) события В, вычисленной при условии наступления с ненулевой вероятностью события А называется отношение вероятности пересечения событий А и В к вероятности события А

Р_А(В) = 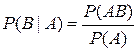(1.22)

При этом полагают, что Р(В) ≠ 0.

Часто условную вероятность p(B|A) можно легко найти из условия задачи, в более сложных случаях приходится пользоваться определением (1.22).

Пример 1.49. В урне лежит N шаров, из них n белых. Из нее достают шар и, не кладя его обратно (выборка без возвращения), достают еще один. Чему равна вероятность того, что оба шара белые?

Решение. Обозначим события: А ={ первым вынули белый шар}, В ={ первым вынули черный шар}, С = {вторым вынули белый шар}. Тогда

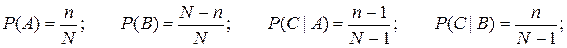
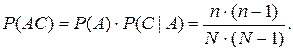
Легко видеть, что вероятность того, что три вынутые подряд (без возвращения) шара белые: 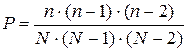и т.д.

Пример 1.50. Из 30 экзаменационных билетов студент подготовил только 25. Если он отказывается отвечать по первому взятому билету (которого он не знает), то ему разрешается взять второй. Определить вероятность того, что второй билет окажется счастливым.

Решение. Пусть события: А={первый вытащенный билет оказался для студента «плохим»}, В={второй билет оказался «хорошим»}. Поскольку после наступления события А один из «плохих» уже извлечен, то остается всего 29 билетов, из которых 25 студент знает. Отсюда искомая вероятность, предполагая, что появление любого билета равновозможно и они обратно не возвращаются, равна p(B|A) = 25/29.

Домашнее задание: ДР-4 ( №1.25,Письменный, стр. 38)