Безусловная оптимизация одной переменной

Нахождение оптимума функции одной переменной f(x) при наложении ограничений типа (28.4) не вызывает затруднений и сводится к нахождению значений f(x) в точках a и b, корней уравнения 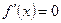(т. е. точек подозрительных на экстремум), а также анализу поведения 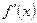в окрестностях этих точек, либо исследованию в них знаков старших производных.

Для многих конкретных задач одномерной оптимизации рационально использовать численные методы нахождения экстремумов. В ряде случаев, когда исходя из физической сущности рассматриваемой задачи известно, что функция f(x) на отрезке [a, b] имеет единственный экстремум целесообразно применять методы исключения интервалов. Основное достоинство методов исключения интервалов – отсутствие необходимости в информации о гладкости исследуемой целевой функции. Недостатком является отсутствие учета величин разностей между вычисляемыми значениями целевой функции, так как это позволило бы ускорить поиск оптимума функции.

В теории математической оптимизации разработан ряд методов позволяющих учитывать эту информацию, однако они требуют от целевой функции определенной степени гладкости.

Наиболее просты в применении методы оптимизации, основанные на полиномиальной апроксимации целевой функции. Идея этих методов состоит в вычислении значений целевой функции в ряде точек исследуемого отрезка и построении на основе результатов таких вычислений аппроксимирующего полинома, чаще всего для этого используется квадратичная экстраполяция. Далее разыскивают оптимум построенного полинома и отождествляют полученное значение с искомым оптимумом целевой функции.

Лекция №30